Integrasyong Lebesgue
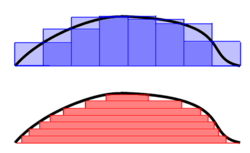
Sa matematika, ang integral ng isang hindi negatibong punsiyon ay maaaring ituring sa pinakasimpleng kaso bilang ang area sa pagitan ng grapo ng punsiyong ito at ang x aksis. Ang integrasyong Lebesgue ay isang konstruksiyong matematikal na nagpapalawig ng integral sa isang mas malaking klase ng mga punsiyon. Ito ay nagpapalawig rin ng mga sakop kung saan ang mga punsiyong ito ay inilarawan. Ito ay gumagampan ng isang mahalagang papel sa sangay ng matematikang tinatawag na real na analisis at sa iba pang mga larangan ng matematika. Ito ay ipinangalanan sa matematikong si Henri Lebesgue na nagpapakilala nito noong 1904. Ito ay isang mahalaga ring bahagi ng aksiyomatikong teoriya ng probabilidad.
Inimbento ni Lebesgue ang isang bagong paraan ng integrasyon. Sa halip ng paggamit ng mga area ng parihaba na pumopokus sa sakop ng punsiyon, tiningnan ni Lebesgue ang kapwa-sakop ng punsiyon para sa kanyang pundamental na unit ng area. Ang ideya ni Lebesgue ay magtayo muna ng integral para sa kanyang tinatawag na mga simpleng punsiyon na mga masusukat na punsiyon na kumukuha lamang ng mga may hangganang maraming halaga. Pagkatapos ay kanyang inilarawan ito para sa mas komplikadong mga punsiyon bilang pinakamaliit na itaas na pagtatakda ng lahat ng mga integral ng simpleng punsiyon na mas maliit sa punsiyong isinasaalang alang. Ang integrasyon ni Lebesgue ay may katangiang ang bawat tinatakdaang punsiyon na inilarawan sa ibabaw ng isang tinatakdaang interbal na may integral na Riemann ay mayroon ring integral na Lebesgue at para sa mga punsiyon ang dalawang mga integral na ito ay magkaayon. Gayunpaman, mayroon maraming mga punsiyon na may integral na Lebesgue na walang integral na Riemann. Bilang bahagi ng pagpapaunlad ng integrasyong Lebesgue, inimbento ni Lebesgue ang konsepto ng sukat na nagpapalawig ng ideya ng haba mula sa mga interbal tungo sa isang napakalaking klase ng mga hanayna tinatawag na mga masusukat na hanay. Ang paraan ni Lebesgue sa paggawa ng isang sukat sa isang integral ay madaling lumalhat sa maraming ibang mga sitwasyon na tumungo sa modernong larangan ng teoriya ng sukat. Upang ilarawan ang integral na Lebesgue ng pormal ay nangangailangan ng nosyon ng sukat na nag-uugnay sa bawat hanay na A ng mga real na bilang ng isang hindi negatibong bilang na na kumakatawan sa sukat ng A. Ang nosyong ito ng sukat ay dapat umayon sa karaniwang haba ng interbal o hindi magkasanib na unyon ng mga interbal. Ipagpalagay na ang ay isang hindi negatibong may halagang real na punsiyon. Gamit ang pagpapartisyon ng saklaw ng f, ang integral ng f ay dapat ang suma sa ibabaw ng t ng mga area sa pagitan ng isang manipis na pirasong horisontal sa pagitan ng and . Ang area na ito ay isa lang . Itakda ang . Ang integral na Lebesgue ng f ay inilalarawan naman ng [1]
kung saan ang integral sa kanan ay isang ordinaryong hindi angkop na integral na Rieman. Para sa angkop na klase ng mga punsiyon(mga masusukat na punsiyon), ito ay naglalarawan ng integral na Lebesgue. Ang isang pangkalahatan(hindi kinakailangang positibong) punsiyong f ay maiintegrado ng Lebesgue kung ang area sa pagitan ng grapo ng f at ang aksis na x ay may hangganan:
Sa kasong ito, ang integral gaya ng sa kasong Riemann, ang pagkakaiba sa pagitan ng area sa itaas na aksis na x at ang area sa ilalim ng aksis na x:
kung saan ang
Konstruksiyon[baguhin | baguhin ang wikitext]
Ito ay nagsisimula sa isang espasyong sukat (E, X, μ) kung saan E ay isang hanay, ang X ay isang σ-alhebra ng mga subpangkat ng E at ang μ ay isang hindi negatibong sukat sa E na inilalarawan sa mga hanay ng X. Halimbawa, ang E ay maaaring epasyong-n na Euclidean na Rn o isang masusukat na Lebesgue na subpangkat nito, ang X ang σ-alhebra ng E, at ang μ ang sukat Lebesgue. Sa teoriya ng probabilidad, ang pag-aaral ay nililimita sa sukat ng probabilidad μ na sumasapat sa. Sa teoriya ng Lebesgue, ang mga integral ay nilalarawan para sa isang klase ng mga punsiyong tinatawag na mga masusukat na punsiyon. Ang isang ƒ ay masusukat kung ang pre-imahe ng bawat interbal ng anyong ay nasa X:
Maipapakita na ito ay katumbas ng pag-aatas ng pre-imahe ng anumang subpangkat na Borel ng R na nasa X. Ang hanay ng mga masusukat na punsiyon ay sarado sa ilalim ng mga operasyong alhebraiko ngunit sa mas mahalaga, ang klase ay sarado sa ilalim ng iba't ibang mga uri ng sa puntong mga hangganang sekwensiyal:
ay masusukat kung ang orihinal na sekwensiya(ƒk)k kung saan ang k ∈ N, ay binubuo ng mga masusukat na punsiyon.
Mga sanggunian[baguhin | baguhin ang wikitext]
Bibliyograpiya[baguhin | baguhin ang wikitext]
- Bartle, Robert G. (1995). The elements of integration and Lebesgue measure. Wiley Classics Library. New York: John Wiley & Sons Inc. xii+179. ISBN 0-471-04222-6. MR 1312157.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (tulong)
- Bourbaki, Nicolas (2004). Integration. I. Chapters 1–6. Translated from the 1959, 1965 and 1967 French originals by Sterling K. Berberian. Elements of Mathematics (Berlin). Berlin: Springer-Verlag. xvi+472. ISBN 3-540-41129-1. MR 2018901.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (tulong)
- Dudley, Richard M. (1989). Real analysis and probability. The Wadsworth & Brooks/Cole Mathematics Series. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software. xii+436. ISBN 0-534-10050-3. MR 0982264.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (tulong) Very thorough treatment, particularly for probabilists with good notes and historical references.
- Folland, Gerald B. (1999). Real analysis: Modern techniques and their applications. Pure and Applied Mathematics (New York) (Second pat.). New York: John Wiley & Sons Inc. xvi+386. ISBN 0-471-31716-0. MR 1681462.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (tulong)
- Halmos, Paul R. (1950). Measure Theory. New York, N. Y.: D. Van Nostrand Company, Inc. pp. xi+304. MR 0033869. A classic, though somewhat dated presentation.
- Lebesgue, Henri (1904). "Leçons sur l'intégration et la recherche des fonctions primitives". Paris: Gauthier-Villars.
{{cite journal}}: Cite journal requires|journal=(tulong)
- Lebesgue, Henri (1972). Oeuvres scientifiques (en cinq volumes) (sa Pranses). Geneva: Institut de Mathématiques de l'Université de Genève. p. 405. MR 0389523.
- Lieb, Elliott; Loos, Michael (2001). Analysis. Graduate Studies in Mathematics. AMS Chelsea. ISBN 978-0821827833.
- Loomis, Lynn H. (1953). An introduction to abstract harmonic analysis. Toronto-New York-London: D. Van Nostrand Company, Inc. pp. x+190. MR 0054173. Includes a presentation of the Daniell integral.
- Munroe, M. E. (1953). Introduction to measure and integration. Cambridge, Mass.: Addison-Wesley Publishing Company Inc. pp. x+310. MR 0053186. Good treatment of the theory of outer measures.
- Royden, H. L. (1988). Real analysis (Third pat.). New York: Macmillan Publishing Company. pp. xx+444. ISBN 0-02-404151-3. MR 1013117.
- Rudin, Walter (1976). Principles of mathematical analysis. International Series in Pure and Applied Mathematics (Third pat.). New York: McGraw-Hill Book Co. pp. x+342. MR 0385023. Known as Little Rudin, contains the basics of the Lebesgue theory, but does not treat material such as Fubini's theorem.
- Rudin, Walter (1966). Real and complex analysis. New York: McGraw-Hill Book Co. pp. xi+412. MR 0210528. Known as Big Rudin. A complete and careful presentation of the theory. Good presentation of the Riesz extension theorems. However, there is a minor flaw (in the first edition) in the proof of one of the extension theorems, the discovery of which constitutes exercise 21 of Chapter 2.
- Saks, Stanisław (1937). "Theory of the Integral". Monografie Matematyczne. 7 (2nd pat.). Warszawa-Lwów: G.E. Stechert & Co.: VI+347. JFM 63.0183.05. Zbl 0017.30004.
{{cite journal}}: Cite journal requires|journal=(tulong); External link in|series=
- Shilov, G. E.; Gurevich, B. L. (1977). Integral, measure and derivative: a unified approach. Translated from the Russian and edited by Richard A. Silverman. Dover Books on Advanced Mathematics. New York: Dover Publications Inc. xiv+233. ISBN 0-486-63519-8. MR 0466463.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (tulong) Emphasizes the Daniell integral.














