Pamparaming Lagrange

Sa matematikal na optimisasyon, ang paraan ng mga pamparaming Lagrange o mga multiplikador na Lagrange (Ingles: Lagrange multiplier) na ipinangalan kay Joseph Louis Lagrange ay nagbibigay ng stratehiya para sa paghahanap ng maxima at minima (mga kasukdulan o dulo't dulo) ng isang punsiyon na nasa ilalim ng mga pagtatakda (constraints).
Halimbawa, tignan isaalang alang ang problema ng optimisasyon na:
- i-maksima (maximize) ang
- sa ilalim ng pagtatakdang(constraint)
Kailangan ipakilala ang bagong bariabulo() na tinatawag na multiplayer na Lagrange at pag-aralan ang punsiyong Lagrange na inilalarawan ng:
kung saan ang terminong ay maaaring idagdag(added) o ibawas(subtracted). Kung ang ay isang maximum para sa orihinal na tinakdaang problema, kung gayon ay may umiiral na kung saan ang ay isang stasyonaryong punto para sa punsiyong Lagrange. Ang mga puntong stasyonaryo ang mga punto kung saan ang mga parsiyal na deribatibo ng Λ ay sero. Gayunpaman, hindi lahat ng mga stasyonaryong punto ay magbibigay ng solusyon sa orihinal na problema. Dahil dito, ang paraan ng mga multiplayer na Lagrange ay magbibigay ng kinakailangang kondisyon para sa optimalidad ng mga tinatakdaang problema.[1][2][3][4][5]
Introduksiyon[baguhin | baguhin ang wikitext]
Ang isa sa pinaka karaniwang mga problema sa kalkulo ang paghahanap ng maxima at minima(sa pangkalahatan ay extrema) ng isang punsiyon ngunit kalimitan ay mahirap na mahanap ang isang saradong anyo para sa isang punsiyong ini-extrema. Ang gayong mga kahirapan ay kalimitang lumilitwa kung nanaisin na i-maxima o i-minima ang isang punsiyon sa ilalim ng isang nakatakdang panglabas na mga kondisyon o constraints. Ang paraan ng mga multiplayer na Lagrange ay isang makapangyarihang kasangkapan sa paglutas ng ganitong klaseng mga problema na hindi nangangailangan ng hayagang paglutas sa mga kondisyon at gagamitin ang mga ito upang tanggalin ang mga ekstrang bariabulo.
Kung isasaalang alan ang dalawang dimensiyonal na problemang nasa itaas na:
- i-maxima(maximize)
- sa ilalim ng pagtatakdang(constraint)
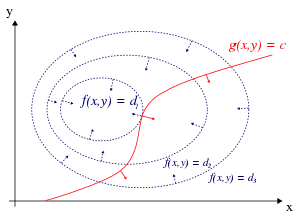
Maaaring ilarawan ang linyang kontur ng f na ibinigay ng:
para sa iba ibang mga halaga ng at ang kontur ng na ibinigay ng .
Ipaglagay na tayo ay naglalakad sa kahabaan ng linyang kontur na may . Sa pangkalahatan, ang mga linyang kontur ng at ay maaaring walang katulad kaya kung susundan ang linyang kontur para sa , maaaring bagtasin(intersect) o tawirin ang mga linyang kontur ng . Ito ay katumbas sa pagsasabi na habang gumagalaw sa kahabaan ng linyang kontur para sa , ang halaga ng ay maaaring magbago. Tanging kung ang linyang kontur para sa ay magtatagpo sa mga linyang kontur ng tangensiyal hindi natin dadagdagan o babawasan ang halaga ng na ang ibig sabihin ay kung ang mga linyang kontur ay nagdadapuan ngunit hindi nagtatawiran.
Ang mga linyang kontur ng f at g ay nagdadapuan kung ang mga bektor na tangent ng mga linyang kontur ay paralelo. Dahil sa ang gradient ng punsiyon ay perpendikular sa mga linyang kontur, ito ay parehas ng pagsasabing ang mga gradient ng f and g ay parelolo. Kaya nais natin ang mga puntong kung saan ang at ang
- ,
kung
at
ang mga respektibong gradient. Ang konstanteng ay kailangan dahil bagaman ang dalawang mga bektor na gradient ay paralelo, ang mga magnitudo ng mga bektor na gradient ay sa pangkalahatan hindi magkatumbas.
Upang pagsamahin ang mga kondisyon ito sa isang ekwasyon, ating ipakikilala ang isang katulong na punsiyong
at lutasin ang
Ito ang paraan ng mga multiplayer na Lagrange. Pansinin na ang ay nagpapahiwatig ng .
Hindi kinakailangang ekstrema[baguhin | baguhin ang wikitext]
Ang tinatakdaang extrema ng ang mga kritikal na punto ng Lagrangian na ngunit ang mga ito ay hindi lokal na ekstrema ng .
Maaaring muling ipormula ang Lagrangian bilang isang Hamiltonian na ang kasong ang mga solusyon ang mga lokal na minima para sa Hamiltonian. Ito ay ginagawa sa teoriyang optimal na kontrol sa anyo ng Prinsipyong minimum ni Pontryagin.
Ang katotohanan ang mga solusyon ng Lagrangiano ay hindi rin kinakailangang extrema ay nagbibigay rin kahirapan para sa numerikal na optimisasyon. Ito ay maaaring matugunan sa pamamagitan ng pagkukwenta ng magnitudo ng gradient dahil sa ang mga sero ng magnitudo ay kinakailangang lokal na minima.
Paghawak ng maraming mga pagtatakda[baguhin | baguhin ang wikitext]


Ang paraan ng mga multiplayer na Lagrange ay maaari ring makitungo sa mga pangmaramihang mga pagtatakda. Upang makita kung paano ito gawin, kailangang muling siyasatin ang problema sa medyo ibang paraan dahil ang konsepto ng "pagtawid" na tinalakay sa taas ay nagiging mabilis na hindi maliwanag kung ating isasaalang-alang mga uri ng pagtatakda na nalilikha kung mayroon tayong higit sa isang pagtatakda na sabay sabay na umaasal. Bilang halimbawa, isaalang alan ang paraboloid na may pagtatakdang isang punto(na maaaring malikha kung may dalawa tayong linyang pagtatakda na nag-uugnayan). Ang hanay na lebel(i.e., linyang kontur) ay maliwanag na lumalabas na tumatawad sa punto ito at ang gradient ay maliwanag na hindi paralelo sa mga gradient ng kahit sa anumang dalawang pagtatakdang linya. Gayunpaman, malinaw na ito ay maximum at minimum dahil may isa lamang punto sa paraboloid na sumasalubong sa pagtatakda.
Bagaman ang halimbawang ito ay tila medyo kakaiba, ito ay madaling maunawaan at kumakatawan sa uri ng epektibong pagtatakda na lumilitaw ng malimit kung makikitungo sa mga nagbabagtasang(intersecting) maraming mga pagtatakda.
Sa buong seksiyon na ito, ang independiyenteng mga bariabulo ay tutukuying ng at bilang isang pangkat ay tutukuyin ang mga ito na . Gayundin, ang punsiyong sinusuri ay tutukuyin na at ang mga pagtatakda ay ikakatawan ng mga ekwasyon na .
Ang basikong ideya ay nanatiling pareho. Kung ating isaalang alang lang ang mga punto na sumasapat sa mga pagtatakda o "nasa" mga pagtatakda, kung gayon, ang puntong ay isang stasyonaryong punto o isang punto na nasa "patag" na rehiyon ng f kung at tanging kung ang mga pagtatakda sa puntong ito ay hindi pumapayag ng paggalaw s a direksiyon kung saan ang f ay hindi nagbabago ng halaga.
Kapag natukoy na ang mga stasyonaryong punto, kailangan tayong magsagawa ng mga karagdagang pagsubok upang makita kung atin nang natuklasan ang minimum, maximum o isa lamang stasyonaryong punto na wala sa mga ito.
Ating sisimulan ang pagsasaalang-alang ng hanay na lebel ng f sa . Ang hanay ng mga bektor na na naglalaman ng mga direksiyon kung saan tayo maaaring makagalawa at mananatili pa rin sa parehong lebel ang mga direksiyon kung saan ang f ay hindi nagbabago o ang pagbabago ay katumbas ng sero. Kaya, sa bawat bektor na v sa ang sumusunod na ugnayan ay dapat totoo:
kung saan ang notasyong sa taas ay nangangahulugang ang bahaging ng bektor na v. Ang ekwasyon sa itaas ay maaaring muling isulat sa mas siksik na heometrikong anyo na makakatulong sa ating intwisyon:
Ginagawa nitong maliwanag na kung tayo ay nasa p, kung gayon ang lahat ng mga direksiyon mula sa puntong ito na hindi nagbabgo ng halaga ng f ay dapat perpendikular sa (ang gradient ng f sa p).
Ngayon, ating isaalang alang ang epekto ng mga pagtatakda. Ang bawat pagtatakda ay naglilimitas ng mga direksiyon na maaari nating galawan mula sa isang partikular na punto at maari pa ring masapatan ang pagtatakda. Maaari nating gamitin ang parehong pamamaraan upang maghanap ng hanay ng mga bektor na na naglalaman ng mga direksiyon na maaari nating galawan at masasapatan pa rin ang pagtatakda. Gaya ng sa itaas, sa bawat bektor na v in , ang sumusunod na ugnayan ay dapat totoo:
Mula dito, makikita nating sa puntong p, ang lahat ng mga direksiyon mula sa puntong ito na sasapat pa rin sa pagtatakdang ito ay dapat perpendikular sa .
Ngayon, handa na tayong pinuhin pa ang ating ideya ng karagdagan at kompletuhin ang paraan: ang isang punto sa f ay isang natatakdaang stasyonaryong punto kung at tanging kung ang direksiyon na nagbabago ng f ay lumalabag sa hindi bababa sa isa sa mga pagtatakda. Makikita nating ito ay totoo dahil kung ang direksiyon na nagbabago ng f ay hindi lumabag sa anumang mga pagtatakda, kung gayon ay may legal na puntong na malapit na may mas mataas o mas mababang halaga para sa f at ang kasalukuyang punto ay kung gayon magiging stasyonaryong punto.
Muling pagbisita sa isang pagtatakda[baguhin | baguhin ang wikitext]
Para sa isang pagtatakda, gagamitin nating ang pangungusap sa itass upang sabihing sa mga stasyonaryong punto, ang direksiyon na nagbabago ng f ay nasa parehong direksiyon na lumalabag sa pagtatakda. Upang matukoy kung ang dalawang bektor ay nasa parehong direksiyon, ating tatandaan na kung ang dalawang mga bektor ay nagmula sa parehong punto at nasa parehong direksiyon, kung gayon, ang isang bektor ay palaging umabot sa isa pa sa pamamagitan ng pagbabago ng haba nito o pagbabaliktad ng punto sa kabaligtarang paraan sa kahabaan ng parehong direksiyon na linya. Sa paraang ito, ating maisasaad na ang dalawang mga bektor ay tumuturo sa parehong direksiyon kung at tanging kung ang isa sa mga ito ay pinarami(multiplied) ng isang real na bilang sa paraang ang mga ito ay magiging magkatumbas sa isa't isa. Kaya para sa ating nilalayon, ating iaatas na:
Kung ating idadagdag ang isa pang kasabay na ekwasyon upang magarantiya na atin lamang isasagawa ang pagsubok na ito kung tayo ay nasa puntong sasapat sa pagtatakda, tayo ay magwawakas sa 2 sabay na mga ekwasyon na kung nalutas ay tutukoy ng lahat ng mga tinakdaang stasyonaryong mga punto:
Pansinin na ang nasa itaas ay isang maikling paraan ng pagsusulat ng mga ekwasyon. Kung buong palalawigin, may mga na magkasabay na mga ekwasyong kailangang lutasin para sa bariabulo na and :
Pangmaramihang mga pagtatakda[baguhin | baguhin ang wikitext]
Para sa higit sa isang pagtatakda, ang parehong pangangatwiran ay lumalapat. Kung may higit sa isang pagtatakda na sabay na aktibo, ang bawat pagtatakda ay nag-aambag sa direksiyon na lalabag dito. Kung pagsasamahin, ang mga paglabag at direksiyon na ito ay bubuo ng epasyong paglabag kung saan ang inpinitesimal na paggalaw sa anumang direksiyon sa loob ng espasyo ay lalabag sa isa o maraming mga pagtatakda. Kaya, upang masapatan ang maraming mga pagtatakda, maaari nating isaad na sa mga stasyonaryong punto, ang direksiyon na nagbabago ng f ay nasa paglabag na espasyo na nilikha ng mga pagtatakdang sabay na umaasal.
Ang espasyong paglabag na nilikha ng mga pagtatakda ay binubuo ng lahat ng mga punto na maaaring maabot sa pamamagitan ng pagdaragdag ng anumang kombinasyon ng may iskala o binaligtad na mga bersiyon ng indibidwal na paglabag na direksiyong mga bektor. Sa ibang salita, ang lahat ng mga punto ay maaabot kung tayo ay gagamit ng indibidwal na paglabag na mga direksiyon bilang basehan ng espasyo. Kaya, maaari na nating maikling maisaad na ang v ay nasa espasyong inilarawan ng kung at tanging kung may umiiral na hanay ng mga multiplayer na na:
na sa ating mga layunin ay maisasalin sa pagsasaad na ang direksiyong nagbabago ng f sa p ay nasa paglabag na espasyong inilalarawan ng mga pagtatakdang kung at tanging kung:
Gaya ng sa una, ating idagdag ang sabay na ekwasyon upang magarantiya na atin lamang isasagawa ang pagsubok na ito kung tayo ay nasa puntong sasapat sa bawat pagtatakda, tayo ay magwakasa sa mga magkasabay na ekwasyon na kung nalutas ay tutukoy sa lahat ng mga tinatakdaang stasyonaryong mga punto:
Ang paraang ito ay kumpleto na ngayon mula sa pananaw ng paglutas ng problema ng paghahanap ng mga stasyonaryong punto ngunit sa kinagagalakang gawin ng mga matematiko, ito ay karagdagan pang mapapaliit sa mas elegant at maikling anyo. Maaaring matalinong napansin ni Lagrange na ang mga ekwasyon sa itaas ay mukhang mga parsiyal na deribatibo ng ilang mas malaking mga skalar na punsiyong L na kumukuha ng lahat ng at lahat ng bilang mga input. Sunod nito, maaaring napansin niyang ang pagtatakda ng bawat ekwasyon na katumbas ng sero ang eksaktong ang gagawin upang malutas ang hindi tinatakdaang mga stasyonaryong mga punto ng mas malaking punsiyon. Sa pinakahuli, kanyang naipakita na ang mas malaking punsiyong L na may mga parsiyal na deribatibong eksaktong ating kailangan ay maaaring likhain ng napaka simple gaya ng:
Sa paglutas ng ekwasyon sa itaas para sa hindi tinatakdaang mga stasyonaryong punto ay lumilikha ng eksaktong parehong mga punto gaya ng paglutas para sa mga tinatakdaang stasyonaryong punto ng f sa ilalim ng mga pagtatakdang .
Bilang parangal kay Lagrange, ang punsiyon sa itaas ay tinatawag na Lagrangian, ang mga skalar na ay tinatawag na Mga Mutliplayer na Lagrange(Lagrange Multipliers) at ang paraang optimisasyong ito ay tinatawag na "Ang paraan ng mga Multiplayer na Lagrange". Ang paraan ng mga multiplayer na Lagrange ay nilalahat ng Mga kondisyong Karush–Kuhn–Tucker na maaaring magsaalang alan ng mga pagtatakdang inekwalidad(hindi magkatumbas) na may anyong h(x) ≤ c.
Mga halimbawa[baguhin | baguhin ang wikitext]

Unang halimbawa[baguhin | baguhin ang wikitext]
Ipagpalagay na nais i-maksima ang na nasa ilalim ng pagtatakdang . Ang posibleng hanay ng unit na bilog at hanay na lebel ng f ay mga linyang diagonal (na may lihis na -1), kaya makikita sa larawan sa kanan na ang maksimum ay umiiral sa , at ang minimum ay umiiral sa.
Sa pormal na paglalarawan, itakda ang , at
Itakda ang deribatibong na magbibigay ng sistema ng mga ekwasyon na:
Gaya ng palagi, ang ekwasyong((iii) dito) ang original na pagtatakda.
Kung pagsasamahin ang dalawang mga ekwasyon, ito ay magbibigay ng (sa hayagan ang , kundi ang (i) ay magbibigay 1 = 0, kaya meron tayong).
Kung ihahalili sa (iii), ito ay magbibigay ng , kaya ang at na nagpapakitang ang mga stasyonaryong punto ay at . Kung lulutasin ang obhektibong punsiyong f sa mga ito ay magbibigay ng
kaya ang maksimum ay na nakamit sa , at ang minimum ay na nakamit sa .
Ikalawang halimbawa[baguhin | baguhin ang wikitext]
Ipagpalagay na nais nating hanapin ang mga halagang maksimum ng
na may kondisyong ang mga koordinatong x at y ay nasa bilog sa palibos ng pinagmula(origin) na may radyus na √3 na nasa ilalim ng pagtatakdang
Dahil sa may isa lamang pagtatakda ay gagamit tayo ng isa lamang pamparami na λ.
Ang pagtatakdang g(x, y)-3 ay katulad ng sero sa bilog ng radyus na √3. Kaya anumang pamparami(multiple) ng g(x, y)-3 ay maaaring idagdag sa f(x, y) nag nag-iiwan sa f(x, y) na hindi nabago sa rehiyon pinag-iinteresan(sa itaas ng bilog nang ating orihinal na pagtatakda ay nasasapatan). Itakda ang:
Ang mga kritikal na halaga ng ay umiiral kung ang gradient nito ay sero. Ang mga parsiyal na deribatibo ay:
Ang ekwasyong (iii) ay isa lamang orihinal na pagtatakda. Ang ekwasyong (i) ay nagpapahiwatig na ang o λ = −y. Sa unang kaso, kung ang x = 0 kung gayon ay dapat mayroon tayong sa pamamagitan (iii) at sa pamamagitan ng (ii) ay λ = 0. Sa ikalawang kaso, kung ang λ = −y at kung ihahali sa ekwasyong (ii) meron tayong:
Pagkatapos ay ang x2 = 2y2. Kung ihahalili sa ekwasyong (iii) at lulutasin ang y ay magbibigay ng halagang ito ng y:
Kaya mayroon anim na mga kritikal na puntong:
Kung lulutasin ang nilalayong punsiyon sa mga puntong ito, ating matatagpuang
Kaya ang nilalayong punsiyon(objective funtion) ay nagkakamit ng global na maksimum(sa ilalim ng mga pagtatakda) sa at ang global na minimum sa Ang puntong ay isang lokal na minimum at ang ay isang lokal na maksium na maaaring matukoy sa pagsasaalang-alang ng Matrix na Hessian ng.
Tandaan na habang ang ay isang kritikal na punto ng , ito ay hindi isang lokal na ekstremum. Mayroon tayong . Sa anumang ibinigay na kapitbahayan ng , maaari tayong pumili ng isang maliit na positibong at isang maliit na ng anumang senyas(sign) upang makamit ang mga halagang na parehong mas malaki at maliit sa .
Mga sanggunian[baguhin | baguhin ang wikitext]
- ↑ Bertsekas, Dimitri P. (1999). Nonlinear Programming (Second pat.). Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0.
- ↑ Vapnyarskii, I.B. (2001), "Lagrange multipliers", in Hazewinkel, Michiel (pat.), Encyclopedia of Mathematics, Springer, ISBN 978-1556080104.
- ↑
- Lasdon, Leon S. (1970). Optimization theory for large systems. Macmillan series in operations research. New York: The Macmillan Company. pp. xi+523. MR 0337317.
- Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan pat.). Mineola, New York: Dover Publications, Inc. pp. xiii+523. MR 1888251.
- ↑
Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "XII Abstract duality for practitioners". Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Bol. 306. Berlin: Springer-Verlag. pp. 136–193 (and Bibliographical comments on pp. 334–335). ISBN 3-540-56852-2.
{{cite book}}: Cite has empty unknown parameter:|2=(tulong); Text "MR1295240" ignored (tulong) - ↑ Lemaréchal, Claude (2001). "Lagrangian relaxation". In Michael Jünger and Denis Naddef (pat.). Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. Bol. 2241. Berlin: Springer-Verlag. pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR 1900016.[[Digital object identifier|doi]]:[//dx.doi.org/10.1007%2F3-540-45586-8_4 '"`UNIQ--nowiki-00000088-QINU`"'].
{{cite book}}: Check|mr=value (tulong); Cite has empty unknown parameter:|1=(tulong); External link in|mr=





























![{\displaystyle {\begin{matrix}\underbrace {\begin{matrix}\left[{\begin{matrix}{\frac {df}{dx_{1}}}\\{\frac {df}{dx_{2}}}\\\vdots \\{\frac {df}{dx_{N}}}\\\end{matrix}}\right]\\{}\\\end{matrix}} _{\nabla f}&\centerdot &\underbrace {\begin{matrix}\left[{\begin{matrix}v_{x_{1}}\\v_{x_{2}}\\\vdots \\v_{x_{N}}\\\end{matrix}}\right]\\{}\\\end{matrix}} _{v}&=\,\,0\\\end{matrix}}\,\,\,\,\,\,\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\,\,\,\nabla f\,\,\,\centerdot \,\,\,\,v\,\,=\,\,\,0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e95ae0621a276e0be7398d99c6798b96536597)




















































