Pamparaming Lagrange: Pagkakaiba sa mga binago
No edit summary |
No edit summary |
||
| Linya 12: | Linya 12: | ||
:<math> \Lambda(x,y,\lambda) = f(x,y) + \lambda \cdot \Big(g(x,y)-c\Big),</math> |
:<math> \Lambda(x,y,\lambda) = f(x,y) + \lambda \cdot \Big(g(x,y)-c\Big),</math> |
||
kung saan ang terminong <math>\lambda</math> ay maaaring idagdag(added) o |
kung saan ang terminong <math>\lambda</math> ay maaaring idagdag(added) o ibawas(subtracted). Kung ang <math>f(x, y)</math> ay isang maximum para sa orihinal na tinakdaang problema, kung gayon ay may umiiral na <math> \lambda</math> kung saan ang <math>(x,y,\lambda)</math> ay isang [[stasyonaryong punto]] para sa punsiyong Lagrange. Ang mga puntong stasyonaryo ang mga punto kung saan ang mga [[parsiyal na deribatibo]] ng Λ ay sero. Gayunpaman, hindi lahat ng mga stasyonaryong punto ay magbibigay ng solusyon sa orihinal na problema. Dahil dito, ang paraan ng mga multiplayer na Lagrange ay magbibigay ng [[kinakailangang kondisyon]] para sa optimalidad ng mga tinatakdaang problema.<ref>{{cite book |
||
| last = Bertsekas |
| last = Bertsekas |
||
| first = Dimitri P. |
| first = Dimitri P. |
||
Pagbabago noong 18:53, 18 Disyembre 2011

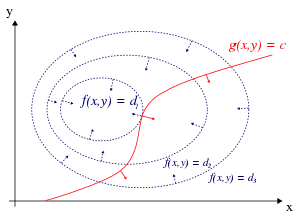
Sa matematikal na optimisasyon, ang paraan ng mga multiplayer na Lagrange(Ingles: Lagrange multiplier) na ipinangalan kay Joseph Louis Lagrange ay nagbibigay ng stratehiya para sa paghahanap ng maxima at minima ng isang punsiyon na nasa ilalim ng mga pagtatakda(constraints).
Halimbawa, tignan isaalang alang ang problema ng optimisasyon na:
- i-maxima(maximize)
- sa ilalim ng pagtatakdang(constraint)
Kailangan ipakilala ang bagong bariabulo() na tinatawag na multiplayer na Lagrange at pag-aralan ang punsiyong Lagrange na inilalarawan ng:
kung saan ang terminong ay maaaring idagdag(added) o ibawas(subtracted). Kung ang ay isang maximum para sa orihinal na tinakdaang problema, kung gayon ay may umiiral na kung saan ang ay isang stasyonaryong punto para sa punsiyong Lagrange. Ang mga puntong stasyonaryo ang mga punto kung saan ang mga parsiyal na deribatibo ng Λ ay sero. Gayunpaman, hindi lahat ng mga stasyonaryong punto ay magbibigay ng solusyon sa orihinal na problema. Dahil dito, ang paraan ng mga multiplayer na Lagrange ay magbibigay ng kinakailangang kondisyon para sa optimalidad ng mga tinatakdaang problema.[1][2][3][4][5]
Sanggunian
- ↑ Bertsekas, Dimitri P. (1999). Nonlinear Programming (Second pat.). Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0.
- ↑ Vapnyarskii, I.B. (2001), "Lagrange multipliers", in Hazewinkel, Michiel (pat.), Encyclopedia of Mathematics, Springer, ISBN 978-1556080104.
- ↑
- Lasdon, Leon S. (1970). Optimization theory for large systems. Macmillan series in operations research. New York: The Macmillan Company. pp. xi+523. MR 0337317.
- Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan pat.). Mineola, New York: Dover Publications, Inc. pp. xiii+523. MR 1888251.
- ↑
Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "XII Abstract duality for practitioners". Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Bol. 306. Berlin: Springer-Verlag. pp. 136–193 (and Bibliographical comments on pp. 334–335). ISBN 3-540-56852-2.
{{cite book}}: Cite has empty unknown parameter:|2=(tulong); Text "MR1295240" ignored (tulong) - ↑ Lemaréchal, Claude (2001). "Lagrangian relaxation". In Michael Jünger and Denis Naddef (pat.). Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. Bol. 2241. Berlin: Springer-Verlag. pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR 1900016.[[Digital object identifier|doi]]:[//dx.doi.org/10.1007%2F3-540-45586-8_4 '"`UNIQ--nowiki-0000001A-QINU`"'].
{{cite book}}: Check|mr=value (tulong); Cite has empty unknown parameter:|1=(tulong); External link in|mr=







