Standard deviation

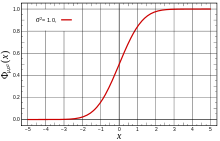
Sa estadistika at teoriya ng probabilidad, ang standard deviation o pamantayang paglihis na kinakatawan ng letrang Griyego na σ ay sumusukat sa pagkakahiwa-hiwalay ng isang frequency distribution. Ang standard deviation ng isang random variable ng isang populasyong pang-estadistika ay ang square root ng variance nito.[1]
Halimbawa[baguhin | baguhin ang wikitext]
Sa isang may hangganang hanay ng bilang, ang standard deviation ang pagkuha ng square root ng aberahe ng mga pagbabawas o diperensiyang kinwadrado mula sa kanilang aberaheng halaga. Halimbawa, ang isang populasyon ay binubuo ng:
kung saan ang aberahe ay 5. Upang kwentahin ang standard deviation ng populasyon, kwentahin muna ang pagbabawas ng ng bawat punto ng datos mula sa aberahe at ikwadrado ang bawat ito:
Kwentahin ang aberahe ng mga ito ay kunin ang square root:
Ang kantidad na ito ang standard deviation ng populasyon at katumbas ng square root ng variance. Ang pormula ay balido lamang kung ang 8 halaga ay bumubuo ng kumpletong populasyon. Kung ang mga halaga ay isang random na sampol mula sa isang populasyon, ito ay hahatiin sa 7 (n−1) sa halip na 8 sa denominator ng huling pormula at ang kantidad ay tatawaging standard deviation ng sampol.



