Teorya ng mga sistemang dinamiko
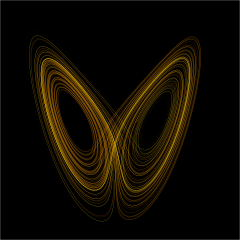
Ang teorya ng mga sistemang dinamikal (Ingles: dynamical systems theory) ay isang sangay ng matematika na ginagamit upang ilarawan ang pag-asal ng mga kompleks na mga sistemang dinamikal na karaniwang gumagamit ng mga ekwasyong diperensiyal o mga ekwasyong diperensiya. Kapag ang mga ekwasyong diperensiyal ay ginamit, ang teorya ay tinatawag na tuloy tuloy na mga sistemang dinamikal. Kapag ang mga ekwasyong diperensiya ay ginamit, ang teorya ay tinatawag na diskretong mga sistemang dinamikal. Kapag ang bariabulo ng panaho ay tumatakbo sa ibabaw ng isang pangkat na diskreto sa loob ng ilang mga interbal at tuloy tuloy sa ibabaw ng ibang mga interbal o kung ang anumang arbitraryong itinakda ng panaho gaya ng isang pangkat na cantor, kung gayon ang isa ay nakakahuha ng mga ekwasyong dinamiko sa mga iskalang panahon. Ang ilang mga sitwasyon ay maaari ring imodelo ng mga halong operador gaya ng mga ekwasyong diperensiyal-diperensiya. Ang teoryang ito ay umuukol sa pangmatagalang kwalitatibong pag-aasal ng mga sistemang dinamikal at nag-aaral ng mga solusyon sa mga ekwasyon ng mosyon ng mga sistema na pangunahing mekanikal sa kalikasan, bagaman ito ay kinabibilangan ng parehong mga oribito ng planeta gayundin ng pag-aasal ng mga sirkitong elektrikal at sa mga solusyon sa parsiyal na ekwasyong diperensiyal na lumilitaw sa biolohiya. Ang karamihan ng modernong pagsasaliksik ay nakapokus sa pag-aaral ng mga sistemang magulo. Ang larangan ng pag-aaral na ito ay tinatawag ring mga sistemang dinamikal, teorya ng mga sistema o ang mas mahabang teoryang matematikal ng mga sistemang dinamikal at ang teoryang matematikal ng mga sistemang dinamikal.
Buod[baguhin | baguhin ang wikitext]
Ang teorya ng mga sistemang dinamikal at teorya ng kaguluhan ay umuukol sa pangmatagalang kwalitatibong pag-aasal ng mga sistemang dinamikal. Dito, ang pokus ay hindi sa paghahanap ng mga tiyak na solusyon sa mga ekwasyon na naglalarawan ng sistemang dinamikal (na kadalasang walang pag-asa) kundi bagkus sa sagot sa mga tanong tulad ng "Ang sistema ba ay tutungo sa nakapirmeng estado sa matagal na panahon, at kung gayon, ano ang mga posibleng nakapirmeng estado?" o "Ang pangmatagalan bang pag-aasal ng sistema ay nakasalalay sa simula nitong kondisyon?" Ang isang mahalagang layunin nito ang paglalarawan ng mga nakapirmeng punto o mga nakapirmeng estado ng isang ibinigay na sistemang dinamikal. Ang mga halagang ito ang mga bariabulo na hindi magbabago sa loob ng panahon. Ang ilan sa mga nakapirmeng punto ito ay nakaaakit na nangangahulugang kung ang sistema ay nagsisimula sa isang malapit na estado, ito ay tutungo sa nakapirmeng punto. Gayundin, ang isa ay interesado sa mga puntong periodiko na mga estado ng sistema na umuulit sa sarili nito pagkatapos ng ilang mga hakbang ng panahon. Ang mga puntong periodiko ay maaari ring nakaaakit. Ang teorema ni Sarkovskii ay isang interesanteng pangungusap tungkol sa bilang mga puntong periodiko ng isang isang-dimensiyonal na diskretong sistemang dinamikal. Kahit ang simpleng mga hindi linyar na sistemang dinamikal ay kadalasang nagpapakita ng halos randoma, kompletong hindi mahuhulaang pag-aasal na tinatawag na kaguluhan. Ang sangay ng mga sistemang dinamikal na nauukol sa malinis na depinisyon at imbestigasyon ng kaguluhan ay tinatawag na teorya ng kaguluhan.
Mga konsepto[baguhin | baguhin ang wikitext]
Mga sistemang dinamikal[baguhin | baguhin ang wikitext]
Ang konseptong sistemang dinamikal ay isang matematikal na pormalisasyon para sa anumang nakapirmeng "patakaran" na naglalarawan ng pagsalalay ng panahon ng isang isang posisyon ng punto sa espasyong nakapaligid nito. Ang mga halimbawa ay kinabibilangan ng mga modelong matematikal na naglalarawan ng pag-ugoy ng isang pendulum ng orasan, ang daloy ng tubig sa isang tubo at ang bilang ng mga isda sa bawat tagsibol sa isang lawa. Ang isang sistemang dinamikal ay may isang estado na tinutukoy ng isang koleksiyon ng mga real na bilang o sa mas pangkalahatan ng isang pangkat ng mga punto sa isang angkop na estadong espasyo. Ang mga bilang ay mga koordinado rin ng isang espasyong heometrikal na isang manipoldo. Ang patakarang ebolusyon ng sistemang dinamikal ay isang nakapirmeng patakaran na naglalarawan kung anong mga panghinaharap na estado ang sumusunod mula sa kasalukuyang estado. Ang patakaran ay deterministiko: para sa isang ibinigay na interbal ng panahon, ang tanging isang estado ay sumusunod mula sa kasalukuyang estado.
Dinamisismo[baguhin | baguhin ang wikitext]
Ang dinamisismo na tinagurian ring hipotesis na dinamiko o ang dinamikong hipotesis sa agham kognitibo o dinamikong kognisyon ay isang bagong pakikitungo sa agham kognitibo na ang halimbawa ang akda ng pilosopong si Tim van Gelder. Ito ay nangangatwirang ang mga ekwasyong diperensiyal ay mas angkop sa pagmomodelo ng kognisyon kesa sa mas tradisyonal na mga modelo ng kompyuter.
Sistemang hindi linyar[baguhin | baguhin ang wikitext]
Sa matematika, ang isang sistemang hindi linyar ay isang sistema na hindi linyar na nangangahulugan isang sistema na hindi sumasapat sa prinsipyong superposisyon. Sa hindi teknikal na paglalarawan, ang sistemang hindi linyar ay anumang problema kung saan ang bariabulo o mga bariabulo na nilulutas ay hindi maisusulat bilang isang sumang linyar ng mga independiyenteng bahagi. Ang hindi pantay na sistema na linyar maliban sa presensiya ng punsiyon ng mga independiyenteng bariabulo ay hindi linyar ayon sa striktong depinisyon ngunit ang gayong mga sistema ay kadalasang pinag-aaralan kasama ng mga sistemang linyar dahil ang mga ito ay pwedeng baguhin sa sistemang linyar basta ang partikular na solusyon ay alam.
Mga kaugnay na larangan[baguhin | baguhin ang wikitext]
Dinamikang aritmetiko[baguhin | baguhin ang wikitext]
- Ang dinamikang aritmetiko ay isang larangan na lumitaw noong mga 1990 na nagsasama ng dalawang sakop ng matematika na mga sistemang dinamikal at teorya ng bilang. Sa klasiko, ang diskretong dinamika ay tumutukoy sa pag-aaral ng paulit ulit na punsiyon ng mga sariling-mapa ng planong kompeks o real na linya. Ang dinamikang aritmetiko ang pag-aaral ng mga katangiang bilang teoretiko ng intedyer, rasyonal, p-adic, at/o mga punto alhebraiko sa ilalim ng paulit ulit aplikasyon ng polinomial o punsiyong rasyonal.
Teorya ng kaguluhan[baguhin | baguhin ang wikitext]
- Ang teorya ng kaguluhan ay naglalarawan ng pag-aasal ng ilang mga sistemang dinamikal na mga sistemang ang estado ay nag-eebolb sa panahon na maaaring magpakita ng mga dinamika na mataas na sensitibo sa mga simulang kondisyon (na kilalang tinagurian na epektong paru-paro). Bilang resulta ng sensitibidad na ito na nagpapamalas sa sarili nito bilang isang paglagong eksponensiyal ng mga perturbasyon ng mga simulang kondisyon, ang pag-aasal ng mga sistemang magulo ay lumilitaw na randoma. Ito ay nangyayari bagaman ang mga sistemang ito ay deterministiko na nangangahulugang ang mga panghinaharap na dinamiko nito ay buong inilalarawan ng mga simulang kondisyon nito na walang nasasangkot na mga elementong randoma. Ang pag-aasal na ito ay tinatawag na deterministikong kaguluhan o simpleng kaguluhan.
Mga sistemang kompleks[baguhin | baguhin ang wikitext]
- Ang mga sistemang kompleks ay isang larangang siyentipiko na nag-aaral ng mga karaniwang katangian ng mga sistemang itinuturing na kompleks sa kalikasan, lipunan at agham. Ito ay tinatawag ring teorya ng mga sistemang kompleks, agham ng kompleksidad, pag-aaral ng mga sistemang kompleks at/o agham ng kompleksidad. Ang mga mahalagang problema ng gayong mga sistema ang mga kahirapan sa mga pormal na pagmomodelo at simulasyon ng mga ito. Mula sa gayong perspektibo sa iba't ibang mga kontekstong pagsasaliksik, ang mga sistemang kompleks ay inilalarawan sa batayan ng kanilang mga iba't ibang katangian.
Teorya ng kontrol[baguhin | baguhin ang wikitext]
- Ang teorya ng kontrol ay isang interdisiplinaryong sangay ng inhinyerya at matematika na umuukol sa pag-iimpluwensiya ng pag-aasal ng mga sistemang dinamikal.
Teoryang ergodiko[baguhin | baguhin ang wikitext]
- Ang teoryang ergodiko ay isang sangay ng matematika na nag-aaral ng mga sistemang dinamikal na may hindi nagbabagong sukat at mga kaugnay na problema. Ang simulang pagkakabuo nito ay naudyukan ng mga problema ng pisikang estadistikal.
Punsiyonal na analisis[baguhin | baguhin ang wikitext]
- Ang punsiyonal na analisis (Ingles: functional analysis) ang sangay ng matematika at sa spesipiko ng analisis na matematika na umuukol sa pag-aaral ng mga espasyong bektor at mga operador na umaasal sa mga ito. Ito ay may historikal na mga ugat sa pag-aaral ng mga espasyong punsiyonal sa partikular ang mga transpormasyon ng punsiyon gaya ng transpormang Fourier gayundin gaya sa pag-aaral ng mga ekwasyong diperensiyal at mga ekwasyong integral. Ang paggamit ng salitang punsiyonal ay bumabalik sa kalkulo ng mga bariasyon na nagpapahiwatig ng isang punsiyon na ang argumento ay isang punsiyon. Ang paggamit nito ay itinuturo sa matematiko at pisikong si Vito Volterra at ang pagkakatatag nito ay malaking itinuturo sa matematikong si Stefan Banach.
Mga grapong sistemang dinamikal[baguhin | baguhin ang wikitext]
- Ang konsepto ng mga grapong sistemang dinamikal (GDS) ay maaaring gamitin upang bihagin ang isang malawak na saklaw ng mga proseso na nangyayari sa mga grapo o network. Ang isang pangunahing tema sa analisis na matematikal at komputasyonal ng GDS ay mag-ugnay na kanilang mga katangiang istraktura at mga nagreresultang dinamikang global.
Mga minapang sistemang dinamikal[baguhin | baguhin ang wikitext]
- Ang mga minapang sistemang dinamikal ay isang teoryang matematikal na nag-iimbestiga ng pag-aasal ng mga sistemang dinamikal kung saan ang solusyon ay narestrikto sa isang pagtatakdang pangkat. Ang disiplinang ito ay nagsasalo ng mga koneksiyon at aplikasyon sa parehong mga problemang matematikal na optimisasyon at puntong ekwilibirum at sa daigdig na dinamikal ng daloy sa mga minapang ekwasyong diperensiyal.
Dinamikang simboliko[baguhin | baguhin ang wikitext]
- Ang dinamikang simboliko ang pagsasanay ng pagmomodelo ng isang topolohikal o makinis na sistemang dinamikal ng isang espasyong diskreto na binubuo ng walang hangganang mga sekwensiya ng mga abstraktong simbolo na ang bawat isa ay tumutugon sa isang estado ng sistema na may dinamika (ebolusyon) na ibinigay ng isang operador ng paglipat.
Dinamikang sistema[baguhin | baguhin ang wikitext]
- Ang dinamikang sistema ang pakikitungo sa pag-unawa ng pag-aasal ng mga sistemang kompleks sa loob ng isang panahon. Ito ay umuukol sa panloob na mga feedback na loop at mga pagkaantala ng panahon na umaapekto sa pag-aasal ng buong sistema.[1] Ang gumagawa sa paggamit ng dinamikang sistema na iba mula sa ibang mga pakikitungo sa pag-aaral ng mga sistemang kompleks ang paggamit ng mga feedback na loop at mga stock at daloy. Ang mga elementong ito ay nakatutulong na paglalarawan kung paanong ang tila mga simpleng sistema ay humaharang sa kawalang linyaridad.
Dinamikang topolohikal[baguhin | baguhin ang wikitext]
- Ang dinamikang topolohikal ay isang sangay ng teorya ng mga sistemang dinamikal kung saan ang mga katangiang kwalitatibo, asimptotiko ay pinag-aaral mula sa pananaw ng pangkalahatang topolohiya.
Mga sanggunian[baguhin | baguhin ang wikitext]
- ↑ "MIT System Dynamics in Education Project (SDEP)". Inarkibo mula sa ang orihinal noong 2008-05-09. Nakuha noong 2021-08-06.
