Punsiyon (matematika)
- Para sa ibang gamit, tingnan ang Punsiyon (paglilinaw).

Ang x sa kanan ang bariabulong input na kumakatawan sa isang halaga ipinasok at ang nasa kaliwa na f(x) ang output na inilabas na halaga o resulta ng nakwentang halaga ng punsiyon sa ibinigay na argumentong x.
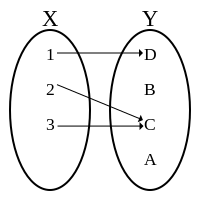
Ang punsiyon[1] (Ingles: function) o bunin [2] sa matematika, ay nag-uugnay ng isang bilang o input (binibigay na bilang) na argumento ng punsiyon, sa halaga ng kalalabasang halaga o output. Ang punsiyon ay nagtatakda lamang ng isang kinalalabasan na output sa isang ipinasok na halaga o input. Ang halaga ng isang punsiyong f na may argumentong x ay tinutukoy ng f(x) at binabasang "f ng x". Ang isang halimbawa ang f(x) = 2x kung saan ang punsiyong f ay nag-uugnay ng input na x sa bilang na dalawang beses na kasing laki nito. Kung ang x = 5, kung gayon ang f(x) = 10.
Ang mga argumento ng punsiyon at halaga ay maaaring mga real na bilang o mga elemento ng anumang ibinigay na pangkat. Halimbawa, ang isang punsiyon ay maaaring mag-ugnay ng letrang A sa bilang na 1, ang letrang B sa bilang na 2 at iba pa. Ang pangkat ng lahat ng mga input para sa isang punsiyon ay tinatawag na sakop (Ingles: domain) at ang pangkat ng lahat ng mga output ang saklaw (Ingles: range) o imahe (Ingles: image) nito.
Maraming mga paraang upang ilarawan o ikatawan ang isang punsiyon gaya ng isang pormula o algoritmo na kumukwenta sa output para sa isang ibinigay na input na isang larawan o grapo ng input-ouput na isinaayos na mga pares ng punsiyon o isang tabla ng mga output sa mga napiling input. Ang isang punsiyon ay maaari ring ilarawan sa pamamagitan ng mga ugnayan nito sa ibang mga punsiyon, halimbawa bilang inbersong punsiyon o solusyon ng isang diperensiyal na ekwasyon. Sa analohiya sa aritmetika, posibleng maglarawan ng punsiyong adisyon, multiplikasyon at ibang mga matematikal na operasyon upang lumikha ng mga bagong punsiyon. Ang isang mahalagang operasyon na inilalarawa sa mga punsiyon ang komposisyon ng mga punsiyon kung saan ang output mula sa isang punsiyon ay nagiging input ng iba pang punsiyon.
Ang mga pormal na depinisyon ng mga punsiyon ay nagbibigay ng pangkat ng mga input (sakop o domain), pangkat ng pinares na input at output at isang pangkat na tinatawag na codomain kung saan ang mga output ay itinakdang mahuhulog. Ang mga kalipunan ng mga punsiyon na may parehong domain at codomain ay tinatawag na mga espasyong punsiyon, na ang mga katangian ay pinag-aaral sa mga matematikal na disiplina gaya ng real na analisis at kompleks na analisis. Ang mga punsiyon at ang iba't ibang mga analogo nito o paglalahat gaya ng mga punktor (Ingles: functor) ng teoriyang kategorya ang mga "sental na bagay ng imbestigasyon" sa karamihan ng mga larangan sa modernong matematika.
Depinisyon[baguhin | baguhin ang wikitext]
Ang isang tiyak na depinisyon ng isang punsiyon ay isang isinaayos na triple ng mga pangkat na isinulat na (X, Y, F) kung saan ang X ang sakop o domain, ang Y ang codomain, at ang F ang pangkat ng mga isinaayos na pares (a, b).[3] Sa bawat mga isinaayos na pares, ang unang elementong a ay mula sa sakop/domain, ang ikalawang elementong b ay mula sa codomain at ang isang kinakailangang kondisyon ay ang bawat elemento sa sakop/domain ang unang elemento sa eksaktong isang isinaayos na pares. Ang pangkat ng lahat ng b ay tinatawag na imahe ng punsiyon at hindi kinakailangang maging buo ng codomain. Ang karamihan sa mga may-akda ay gumagamit ng salitang "range" upang ipakahulugang imahe samantalang ang iba ay gumagamit ng codomain upang pakahulugang range.
Ang notasyong f:X→Y ay nagpapakitang ang f ay isang punsiyn na may sako/domain na X at codomain na Y, at ang punsiyong f ay sinasabing mapa o associate/kaugnay na mga elemento Y.
Imbis na pag-usapan ang isang punsiyonh at tukuyin ang domain at codoamin sa depinisyon nito, normal na mas konbinyenteng pag-usapan ang mga punksiyon na may spesipikong domain at codomai na mga punsiyon ng isang ibinigay na uri at pagkatapos ay ilalarawan ng pangkat ng mga isinaayos na pares na F. Halimbawa, ang isang punsiyon mula sa mga real tungol sa real ay bibigyan ng pangkat ng mga pares na (x, 2x) kung saan ang x ay isang real.
Kung ang domain at codomain ay parehong mga pangkat ng mga real na bilang gaya ng karaniwang kaso, sinasabi nating ang f ay isang may halagang real na punsiyon ng isang real na bariabulo at ang pag-aaral ng mga gayong punsiyon ay tinatawag na mga real na bariabulo. Kung ang domain at codomain ay parehong pangkat ng mga kompleks na bilang, kung gayon, ating sasabihing ang f ay isang may halagang kompleks na punsiyon ng isang kompleks na bariabulo. Ang pag-aaral ng mga punsiyong ito ay tinatawag na mga kompleks na bariabulo. Sa karamihan ng mga sitwasyon, ang domain at codomain ay nauunawan mula sa konteksto at ang tanging ugnayan sa pagitan ng mga input at output ang ibinigay, ngunit kung ang f(x) = √x, kung gayon sa mga real na bariabulo, ang sakop/domain ay limitado sa hindi-negatibong mga bilang samantalang sa mga kompleks na bariabul, ang domain ang lahat ng mga kompleks na bilang.
Lalo na sa teoriya ng pangkat, ang isang punsiyong f ay kalimitang inilalarawan bilang pangkat ng mga isinaayos na pares. Ang domain ay simpleng ang pangkat ng elemento na lumalabas bilang unang elemento ng pares at walang hayagang codomain na hiwalay mula sa imahe.
Ang isang punsiyon ay maaari ring tawaging mapa o pagmamapa/mapping. Gayunpaman, ang ilang mga may-akda ay gumagamit ng mga terminong "punsiyon" at "mapa" upang tukuyin ang iba't ibang uri ng mga punsiyon. Ang ibang mga spesipikong uri ng mga punsiyon ay kinabibilangan ng punsiyonal(Ingles: functional) at mga operador(Ingles: operator).
Ang isang spesipikong input sa isang punsiyon ay tinatawag na argumento ng punsiyon. Sa bawat argumentong halagang x, ang tumutugong walang katulad(unique) na y sa codomain ay tinatawag na halaga sa x, output ng ƒ para sa argumentong x o ang imahe ng x sa ilalim ng ƒ. Ang imahe ng x ay maaaring isulat bilang ƒ(x) o bilang y.
Ang grapo ng punsiyon ang pangkat nito ng mga isinaayos na pares na F. Ito ay isang abstraksiyon ng ideya ng grapo bilang larawan na nagpapakita ng punsiyon na binalangkas sa isang pares ng mga aksis na koordinado. Halimbawa, ang (3, 9), ang punto sa taas ng 3 sa horisontal na aksis sa kanan at 9 sa bertikal na aksis ay nakahimlay sa grapo ng .
Ang sakop/domain na X ay maaaring void ngunit kung ang X = ∅, kung gayon ang F = ∅. Ang codomain na Y ay maaari ring void, ngunit kung ang Y = ∅, kung gayon ang X = ∅ at ang F = ∅. Ang mga gayong walang lamang punsiyon ay hindi karaniwan ngunit ang teoriya ay nagsisiguro ng eksistensiya ng mga ito.
Ang pangkat ng lahat ng mga punsiyong f:X→Y ay minsang tinutukoy ng iYX. Kung ang X ay inpinido(infinite) at mayroon higit sa isang elemnto sa Y, kung gayon mayroon hindi mabibilang na maraming mga punsiyon mula sa X tungo sa Y bagaman ang taning mabibilang marami sa mga ito ang maaaring ihayag ng isang pormula o algoritmo.
Sa mga ilang bahagi ng matematika, kabilang ang teoriya ng rekursiyon at punsiyonal na analisis, konbinyenteng pag-aralan ang mga parsiyal na punsiyon kung saan ang ilang mga halaga ng domain ay walang kaugnayan/association sa grapo, i.e. isang-halagang mga ugnayan. Halimbawa, ang punsiyon f upang ang f(x) = 1/x ay hindi naglalarawan ng isang halaga para sa x = 0, at kaya ay isa lamang parsiyal na punsiyon mula sa real na linya tungo sa real na linya. Ang terminong kabuuang punsiyon ay maaaring gamitin upang bigyang diin ang katotohanang ang bawat elemento ng domain ay lumilitaw bilang unang elemento ng isinaayos ng pares sa grapo. Sa ibang mga bahgai ng matematika, ang hindi-isang-halagang mga ugnayan ay katulad ding isinanib sa mga punsiyon. Ito ay tinatawag na mga maraming halagang punsiyon na may tumutugong terminong isang-halagang punsiyon para sa mga ordinaryong punsiyon.
Maraming mga operasyon sa teoriya ng pangkat gaya ng kapangyarihang pangkat ay may klase ng lahat ng mga pangkat bilang domain ng mga ito at kaya bagaman ang mga ito ay inpormal na inilalarawan bilang mga punsiyon, ang mga ito ay hindi nagkakasya sa set-teoretikal na depinisyon ibinalangkas sa itaas dahil ang klase ay hindi kinakailangang isang pangkat.
Ang punsiyon ay isang espesyal na kaso ng mas pangkalahatang matematikal na konseptong relasyon(ugnayan) kung saan ang restriksiyon ang bawat elemento ng domain ay lumilitaw na unang elemento sa isa at tanging isang isinaayos na pares lamang inalis. Sa ibang salita, ang elemento ng domain ay maaaring hindi unang elemento ng anumang isiniaayos na pares o maaaring unang elemento ng dalawa o higit pang isinaayos na pares. Ang relasyon ay "may isang halaga" kapag kung ang elemento ng domain ang unang elemento, ito ay hindi unang elemento ng anumang ibang isinaayos na pares. Ang relasyon ay isang "kaliwang-kabuuan" o simpleng "kabuuan" kung ang bawat elemento ng domain ang unang elemento ng isang isinaayos na pares. Kaya ang punsiyon ay isang buon, may isang halagang relasyon.
Notasyon[baguhin | baguhin ang wikitext]
Ang pormal na deskripsiyon ng isang punsiyon ay karaniwang sumasangkot sa pangalan ng punsiyon, sakop/domain nito, codomain nito at isang patakarang ng tugunan(correspondence). Kaya kalimitan nating nakikita ang isang dalawang-bahaging notasyon na ang halimbawa ang
kung saan ang unang bahagi ay binabasang:
- Ang "ƒ ay isang punsiyon mula sa N tungo sa R" (kalimitang isinulat na "Let (hayaan) ang ƒ: X → Y" upang pakahulugang "Hayaang ang ƒ ay maging isang punsiyon mula sa X tungo sa Y"), o
- "ƒ ay isang punsiyon sa N sa R'", o
- "ƒ ay isang may halagang-R-na punsiyon ng isang may halagang-N na bariabulo",
at ang ikalawang bahagi ay binabasang:
- ay namamapa sa
Dito, ang punsiyong pinangalanang "ƒ" ay may mga natural na bilang bilang sakop/domain, real na bilang bilang codoamin at nagmamapa ng n sa sarili nito na hinati ng π. Sa hindi pormal na paglalarawan, ang mahabang anyong ito ay maaaring paiklin na
kung saan ang f(n) ay binabasa bilang "f bilang punsiyon ng n" o "f ng n". Mayroon ilang pagkawala ng impormasyon: hindi na natin hayagang ibinibigay ang domain na N at codomain na R.
Karaniwang inaalis ang parentheses sa palibot ng argumento kapag walang walang maliit na tsansa ng pagkalito kaya sin x. Ito ay tinatawag na notasyong prefix. Ang pagsusulat ng punsiyon pagkatapos ng agumento gaya ng sa x ƒ, ay tinatawag na notasyong postfix. Halimbawa, ang paktoryal na punsiyon ay kinagagawiang isulat na n! bagaman ang paglalahat nito na punsiyong gama ay isinusulat na Γ(n). Ang mga parenteheses ay ginagamit par rin upang lutasin ang mga kalituhan at tumukoy ng pangunguna(precedence) bagaman sa ilang mga pormal na pagtatakda, ang konsistenteng paggamit ng notasyong prefix o postfix ay nag-aalis ng pangangailangan para sa anumang parentheses.
Upang ilarawan ang isang punsiyon, ang notasyong tuldok(dot notation) ay minsang ginagmait upang bigyang diin ang punsiyonal na kalikasan ng ekspresyon ng hindi nagtatakda ng espesyal na simbol sa baribaulo. Halimbawa, ang ay tumatayo para sa punsiyong , ang ay tumatayo para sa punsiyong integral at iba pa.
Mga uri ng punsiyon[baguhin | baguhin ang wikitext]
Elementaryang mga punsiyon[baguhin | baguhin ang wikitext]
Elementaryang mga punsiyon ay mga punsiyon na nilikha para sa mga pundamental na operasyon ng matematika gaya ng adisyon, substraksiyon, multiplikasyon at dibisyon.
Mga punsiyong alhebraiko[baguhin | baguhin ang wikitext]
- Polinomial
- Linyar na punsiyon: Unang digri na polinomial, ang grap ay diretsong linya graph is a.
- Kwadratiko na punsiyon: Ikalawang digri na polinomial, ang grap ay parabola.
- Kubiko na punsiyon: Ikatlong digri na polinomial.
- Kwartiko na punsiyon: Ikaapat na digri na polinomial
- Kwintiko na punsiyon: Ikalimang digri na polinomial.
- Sekstiko na punsiyon: Ikaanim na digri na polynomial.
- Rasyonal na punsiyon: rasyo ng dalawang polinomial.
- ika n na ugat
Mga elementaryang transendental na punsiyon[baguhin | baguhin ang wikitext]
- Eksponensiyal na punsiyon
- Hyperboliko na punsiyon
- Logaritmo
- Kapangyarihang punsiyon
- Peryodikong mga punsiyon
Mga sanggunian[baguhin | baguhin ang wikitext]
- ↑ Salin ng function
- ↑ Marissa R. Enriquez (2012). English-Tagalog Tagalog-English Dictionary. Amos Books, Inc. p. 424. ISBN 971-0324-24-1.
- ↑ Ethan D Bloch (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. p. 131. ISBN 978-1-4419-7126-5.