Distribusyong normal
Probability density function The red curve is the standard normal distribution | |
Cumulative distribution function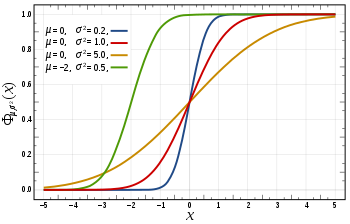 | |
| Notation | |
|---|---|
| Parameters | μ ∈ R — mean (location) σ2 > 0 — variance (squared scale) |
| Support | x ∈ R |
| CDF | |
| Mean | μ |
| Median | μ |
| Mode | μ |
| Variance | |
| Skewness | 0 |
| Ex. kurtosis | 0 |
| Entropy | |
| MGF | |
| CF | |
Sa teoriya ng probabilidad, ang distribusyong normal (o Gaussian) ay isang tuloy tuloy na distribusyong probabilidad na may hugis-kampanang punsiyong probabilidad na densidad na kilala bilang punsiyong Gaussian o sa hindi pormal na paglalarawan ay kurbang kampana o bell curve.[1]
Ang paremetrong μ ang mean o inaasahan(lokasyon ng tuktok) at ang σ 2 ang bariansa. Ang σ ay kilala bilang pamantayang paglihis. Ang distribusyong mayroong μ = 0 at σ 2 = 1 ay tinatawag na pamantayang distribusyong normal o ang unit na distribusyong normal. Ang isang distribusyong normal ay kadalasang ginagamit bilang ang unang aproksimasyon upang ilarawan ang isang may halagang real na randomang bariabulo na nagkukumpol sa palibot ng isang halagang mean. Ang distribusyong normal ay itinuturing na pinakakilalang distribusyong probabilidad sa estadistika. May ilang mga dahilan para dito:[2] Una, ang distribusyong normal ay lumilitaw mula sa teoryang sentral na hangganan na nagsasaad na sa ilalim ng mga katamtamang kondisyon, ang mean ng isang malaking bilang ng mga randomang bariabulo na hinugot mula sa parehong distribusyon ay ipinamahagi ng mga normal nang hindi isinasaalang ang anyo ng orihinal na distibusyon. Ito ay nagbibigay rito ng ekspepsiyonal na malawak na aplikasyon halimbawa sa pagsasampol. Ikalawa, ang distribusyong normal ay labis na mapapangasiwaan na ang ibig sabihin ang isang malaking bilang ng mga resulta na sumasangkot sa distribusyong ito ay maaaring hanguin sa isang hayagang anyo. Dahil dito, ang distribusyong normal ay karaniwang na-eenkwentro sa pagsasanay at ginagamit sa buong estadistika, natural na agham at panlipunang agham[3] bilang isang simpleng modelo para sa komplikadong phenomena. Halimbawa, ang oberbasyonal na pagkakamali sa isang eksperimento ay karaniwang ipinagpapalagay na sumusunod sa isang distribusyong normal at ang propagasyon ng kawalang katiyakan ay kinukwenta gamit ang asumpsiyong ito. Panisin na ang isang bariabulong nasa distibriusyong normal ay may simetrikong disribusyon sa mean nito. Ang mga kantidad na lumalago ng ekponensiyal gaya ng mga presyo, sahod o populasyon ay kadalasan humihilig sa kanan at kaya ay mas mabuting ilarawan ng ibang mga distribusyon gaya ng distribusyong log-normal o distribusyong Pareto. Sa karagdagan, ang probabilidad na makita ang isang halagang nasa distribusyong normal na malayo(i.e. higit s ailang mga pamantayang paglihis) mula sa mean ay bumagsak ng labis ng mabilis. Bilang resulta, ang inperensiyang estadistikal gamit ang isang distribusyong normal ay hindi malakas sa presensiya ng mga outlier(datos na hindi inaasahang malayo mula sa mean sanhi ng mga eksepsiyonal na sirkunstansiya, oberbasyonal na pagkakamali etc) Kapag ang mga outlier ay inaasahan, ang datos ay mas mabuting ilarawan gamit ang isang mabigay na may buntot na distribusyon gaya ng distribusyong-t ni Student. Mula sa isang perspektibong teknikal, ang mga alternatibong paglalarawan ay posible, halimbawa:
- Ang distribusyong normal ang tanging absolutong tuloy tuloy na ang lahat ng mga kumulante ng lagpas sa unang dalawa(ie iba sa mean at bariansa) ay sero.
- Sa isang ibinigay na mean at bariansa, ang tumutugong distribusyong normal ang tuloy tuloy na distribusyon na may distribusyong maksimum na entropiya.[4][5]
Ang mga distribusyong normal ay isang pang-ilalaim na klase ng mga distribusyong eliptikal
Mga sanggunian
[baguhin | baguhin ang wikitext]- ↑ The designation "bell curve" is ambiguous: there are many other distributions which are "bell"-shaped: the Cauchy distribution, Student's t-distribution, generalized normal, logistic, etc.
- ↑ Casella & Berger (2001, p. 102)
- ↑ "Gale Encyclopedia of Psychology – Normal Distribution". Inarkibo mula sa orihinal noong 2012-07-10. Nakuha noong 2012-07-10.
{{cite web}}: CS1 maint: date auto-translated (link) - ↑ Cover, T. M.; Thomas, Joy A (2006). Elements of information theory. John Wiley and Sons. p. 254.
{{cite book}}: CS1 maint: date auto-translated (link) - ↑ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics. Elsevier: 219–230. Inarkibo mula sa orihinal (PDF) noong 2016-03-07. Nakuha noong 2011-06-02.
{{cite journal}}: CS1 maint: date auto-translated (link)



![{\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04670b14acb4ddb796469f3812ead9d9cccec275)




