Teorya ng grap

Sa matematika at agham pangkompyuter, ang teoriya ng grap (Ingles: graph theory) ay ang pag-aaral ng grap (graph): mga istruktura na ginagamit sa paggawa ng modelo ng mga relasyong pangmagkapares sa pagitan ng mga bagay na nasa isang koleksiyon. Ang grap sa kontekstong ito ay tumutungkol sa isang koleksiyon ng mga taluktok at isang koleksiyon ng mga dulo na nagkokonekta sa pares ng taluktok. Ang grap ay puwedeng walang-direksiyon (undirected) o walang patutunguhan, ibig sabihin hindi pinag-iiba ang dalawang taluktok na kaugnay ng isang dulo. Puwede rin itong maging may patutunguhan (directed), na ang ibig sabihin ay may direksiyon ang gilid nito mula sa isang vertex patungo sa isa pa. Tingnan ang grap (matematika) para sa ibang mas detalyadong kahulugan at ibang uri ng grap na kadalasang pinag-aaralan. Hindi dapat ipagkamali ang mga grap na pinag-aaralan sa teoriyang grap sa mga pampunksiyong grap o mga grap na may-tungkulin (graphs of functions) at iba pang klase ng grap.
Tingnan po ang talasalitaan ng teoriyang grap para sa ilang batayang kahulugan sa teoriyang grap.
Kasaysayan
[baguhin | baguhin ang wikitext]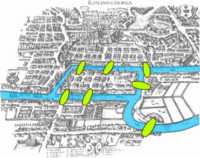
Ang itinuturing na unang panulat sa kasaysayan ng teoriyang grap ay ang akda ni Leonhard Euler hinggil sa Pitong Tulay ng Königsberg na nalathala noong 1736.[1] Itinuloy ng akdang ito at ng isinulat ni Vandermonde hinggil sa problema ng knight ang analysis situs na sinimulan ni Leibniz. Ang pormula ni Euler na nag-uugnay ng bilang ng mga gilid, vertex, at face ng isang convex polyhedron ay pinag-aralan at ginawang pangkalahatan ni Cauchy [2] at L'Huillier,[3]; at siyang simula ng topolohiya.
Pagkatapos ng higit sa isang dantaon matapos ang akda ni Euler hinggil sa mga tulay ng Königsberg at habang ipinakikilala ni Listing ang topolohiya, si Cayley ay nag-aral ng isang partikular na klase ng grap, ang tree. Ito ay bunga ng pag-aaral niya ng mga partikular na anyong pang-analitiko na nagmumula sa diperensiyal na kalkulus. Ang pag-aaral ng mga tree ay maraming implikasyon para sa pangteoriyang kimika. Ang mga ginagamit na teknik dito ay may kinalaman sa enumerasyon ng mga graph na may mga partikular na katangian. kaya ang teoriyang grap na pang-enumerasyon ay nagmula sa resulta ng ginawa ni Cayley at sa pundamental na resultang inilathala ni Pólya sa pagitan ng 1935 at 1937, at ng paggawang pangkalahatan ng mga ito ni De Bruijn noong 1959. Inugnay ni Cayley ang mga resulta niyang nakuha sa mga tree sa kasabayan nitong pag-aaral ng mga komposisyong kimikal.[4] Ang pagsasanib ng mga ideya na nagmula sa matematika at iyong mula sa kimika ay ang ninuno ng ilan sa istandard na terminolohiya sa teoriyang grap. Ang terminong "graph" mismo ay ipinakilala ni Sylvester sa akda niyang nalathala noong 1878 sa Nature.[5]
Ang isan sa pinakatanyag at pinakaproduktibong problema sa teoriyang grap ay ang problema ng apat na kulay: "Totoo ba na ang anumang mapa na iginuhit sa isang patag ay maaaring magkaroon ng mga rehiyon na may apat na kulay, kung saan ang anumang dalawang rehiyon na may magkanugnog na hangganan ay magkaiba ang kulay?". Ang problemang ito ay nanatiling hindi nalulutas sa loob ng mahigit na sandaang taon, at ang patunay na ibinigay nina Kenneth Appel and Wolfgang Haken noong 1976 (pagtiyak sa 1936 na uri ng konpigurasyon na ang pag-aaral ay sapat at ang pagtsek ng katangian ng mga konpigurasyon ito sa pamamagitan ng kompyuter) ay hindi kumumbinsi sa komunidad. Pagkatapos ng dalawampung taon ay isang mas simpleng patunay na nag-aaral sa mas kaunting konpigurasyon ang ibinigay nina Robertson, Seymour, Sanders and Thomas.[6][7][8]
Ang problemang ito ay unang ihinayag ni Francis Guthrie noong 1852 at ang unang nakasulat na rekord ng problemang ito ay nasa isang sulat ni De Morgan na para kay Hamilton noong taong ding iyon. Maraming maling patunay ang iminungkahi kabilang na ang kina Cayley, Kempe, at iba pa. Ang pag-aaral ng paggawang pangkalahatan ng problemang ito nina Tait, Heawood, Ramsey at Hadwiger ay nagbunga ng pag-aaral ng pagkulay sa mga graph na naka-embed sa surface na may arbitraryong genus. Ang repormulasyon ni Tait ay lumikha ng bagong klase ng mga problema, ang mga problema sa paktoralisasyon, na pinag-aralan nina Petersen at Kőnig. Ang mga akda ni Ramsey hinggil sa pagkukulay at lalo pa ang mga resultang nakuha ni Turán noong 1941ay ang ninuno ng isa pang sangay ng teoriyang grap, ang teoriyang grap na extremal.
Ang hiwalay na pag-unlad ng topolohiya mula 1860 hanggang 1930 ay nag-ambag pabalik sa teoriyang grap sa pamamagitan ng mga akda nina Jordan, Kuratowski at Whitney. Ang isa pang importanteng paktor sa magkasamang pag-unlad ng teoriyang graph at topolohiya ay nagmula sa paggamit ng teknik ng modernong alhebra. Ang unang halimbawa ng paggamit na ito ay sa akda ng pisikong si Gustav Kirchhoff, na inilathala noong 1845 ang kanyang batas ng mga circuit ni Kirchhoff na ginagamit sa pagtaya ng boltahe at kuryente sa mga circuit ng elektrisidad.
Ang introduksiyon ng probabilistikong paraan sa teoriyang grap, lalo na sa pag-aaral nina Erdős at Rényi ng asimtotikong probabilidad ng koneksiyon ng mga graph, ay nanganak ng isa pang sangay, na kilala bilang teoriyang graph na walang-pili, na naging mabungang batis ng mga resultang pangteoriyang-grap.
Pagguhit ng mga grap
[baguhin | baguhin ang wikitext]Ang mga grap ay kinakatawan ng larawan sa pamamagitan ng pagguhit ng isang tuldok para sa bawat taluktok, at ang pagguhit ng arko sa pagitan ng bawat taluktok kung konektado ang mga ito ng isang gilid. Kung may direksiyon ang grap, ang direksiyon ay ipapakita sa pamamagitan ng pagguhit ng pana.
Ang pagguhit ng grap ay hindi dapat ipagkamali sa grap mismo (ang abstrakton, di-larawang istruktura) dahil maraming paraan ng paggawa ng istruktura ng pagguhit ng grap. Ang mahalaga lamang ay kung aling taluktok ang konektado sa alin pa, at kung ilang dulo ang nagkukunekta sa kanila; at hindi ang eksaktong layout. Sa praktika mahirap mapagpasiyahan kung kumakatawan sa magkaparehong graph ang dalawang drowing. Depende sa domain ng problema and ilang layout ay maaaring mas mabuti at mas madaling maunawaan kaysa iba pa.
Istruktura ng datos na pangteoriyang grap
[baguhin | baguhin ang wikitext]Maraming paraan ng pagiimbak ng graph sa sistemang pangkompyuter. Ang istruktura ng datos na gagamitin ay nakasalalay sa istruktura ng graph at sa algoritmo na gagamitin sa pagmanipula ng grap. Sa teoriya ay mapag-iiba natin ang listahan at ang matrix na istruktura, pero sa konkretong aplikasyon ang pinakamahusay na istruktura ay kadalasang kombinasyon ng dalawa. Ang listahang istruktura ay karaniwang mas naiibigan para s amga sparse graph dahil mas maliit ang kailangan nilang memorya. Sa kabilang banda mas nagbibigay ng mas mabilis na access para sa ilang aplikasyon ang mga matrix na istruktura pero gumagamit ng maraming memorya.
Istrukturang listahan
[baguhin | baguhin ang wikitext]- Incidence na listahan
Ang mga edge ay kinakatawan ng isang array na naglalaman ng mga pares (naka-order kung directed) ng vertex (na pinagkokonekta ng edge) at marahil ay timbang at iba pang datos. Ang mga vertex na pinagkokonekta ng isang edge ay sinasabing adjacent.
- Adjacency na listahan
Katulad ng incidence na listahan, ang bawat vertex ay may listahan ng kung aling vertex ito naka-adjacent. Nagbubunga ito ng dobleng datos sa isang undirected na graph: Halimbawa, kung ang vertex A at B ay adjacent, ang listahan ng adjancency ng A ay naglalaman ng B, samantalang ang listahan ng B ay naglalaman ng A. Ang mga query ng adjacency ay mas mabilis pero mas maraming espasyo ng imbakan ang kailangan.
Istrukturang Matris (matrix)
[baguhin | baguhin ang wikitext]- Insidensiyang matris
Ang graph ay kinakatawan ng matris na may laking |V| (bilang ng mga vertex) sa |E| (bilang ng edge) kung saan ang tala na [vertex, edge] ay naglalaman ng datos ng mga dulo ng edge (pinakasimpleng kaso: 1 - konektado, 0 - di konektado).
- Adjacency ng matris
Ito ang n sa n na matris A, kung saan ang n ay ang bilang ng taluktok sa grap. Kung may dulo mula sa isang taluktok x papunta sa isang taluktok y, ang elementong ay 1 (o sa pangkalahatan ay ang bilang ng mga xy na dulo), kung hindi ay 0 ito. Sa pagtuos, napapadali ng matris na ito ang paghahanap ng mga subgraph, at ang pagbaligtad ng isang directed na grap.
- Laplacian na matris o Kirchhoff na matris o Admittance na matris
Ang kahulugan nito ay D − A, kung saan ang D ay ang diagonal degree matrix. Lantaran nitong ihinahayag ang impormasyon ng adjacency at impormasyon ng antas.
- Distansiyang matris
Isang simetrikong n sa n na matris D, na ang elementong ay ang haba ng pinakamagsing path sa pagitan ng x at y; kung walang ganitong path ang = infinity. Makukuha ito mula sa mga power ng A:
Mga suliranin sa teoriyang graph
[baguhin | baguhin ang wikitext]Enumerasyon
[baguhin | baguhin ang wikitext]Maraming panitikan hinggil sa panggraph na enumerasyon: ang problema ng pagbibilang ng mga graph na nakakasunod sa ilang itinakdang kondisyon. Ang ilan sa mga gawang ito ay matatagpuan kina Harary at Palmer (1973).
Mga subgraph, induced subgraph, at minor
[baguhin | baguhin ang wikitext]Ang isang karaniwang problema na tinatawag na problemang subgraph isomorphism ay ang paghahanap ng fixed graph bilang subgraph sa isang ibinigay na graph. Ang isang dahilan kung bakit nakakaakit ang ganitong tanong ay dahil maraming katangian ng graph ang namamana sa mga subgraph, ibig sabihin ang isang graph ay may isang katangian kung at tangi kung lahat ng subgraph, o lahat ng induced subgraph, ay mayroon ding ganitong katangian. Kaya lamang ang paghahanap ng maximal na subgraph na may isang uri ay kadalasang isang problemang NP-complete.
- Ang paghahanap ng pinakamalaking kumpletong graph ay tinatawag na problemang clique (NP-complete).
Isa pang kahalintulad nitong problema ay ang paghahanap ng induced subgraphs sa isang ibinigay na graph. Muli, ang ilang importanteng katangian ng graph ay namamana sa induced subgraphs, samakatuwid ang isang graph ay may isang katangian kung at tangi kung ang lahat ng induced subgraphs ay maryroon din ng katangiang ito. Ang paghahanap ng mga maximal induced subgraph na may isang uri ay kadalasan ding NP-complete. Halimbawa,
- Ang paghahanap ng pinakamalaking walang-edge na induced subgraph, o independiyenteng set, na tinatawag na problemang independiyenteng set (NP-complete).
Ang isa pang ganitong uri ng problema, ang problemang minor containment, ay ang paghahanap ng fixed graph bilang minor ng isang ibinigay na graph. Ang minor o subcontraction ng isang graph ay anumang graph na nakuha sa pamamagitan ng pagkuha ng isang subgraph at pag-contract ng ilan (o walang) edge. Maraming katangian ng graph ang namamana sa mga minor, samakatuwid ang isang graph ay may isang katangian lamang tangi kung ang lahat ng minor ay katangian ding ito. Ang isang tanyag na halimbawa ay:
Ang isang graph ay planar kung naglalaman ito bilang isang minor na hindi ang kumpletong bipartite graph (Tingnan ang Tatlong-cottage na problema) o ang kumpletong graph .
Ang isa pang klase ng mga problema ay may kinalaman sa kung hanggan saan ang iba-bang species at paglalahat ng mga graph ang nadedetermina ng kanilang mga point-deleted subgraph, halimbawa:
- Ang reconstruction conjecture
Pagkulay ng grap
[baguhin | baguhin ang wikitext]Maraming problema ang tungkol sa iba-ibang paraan ng pagkulay ng mga graph, halimbawa:
- Ang teorema ng apat na kulay
- Ang teorema ng strong perfect graph
- Ang Erdős-Faber-Lovász conjecture (di pa nalulutas)
- Ang total coloring conjecture (di pa nalulutas)
- Ang list coloring conjecture (di pa nalulutas)
Mga problema ng ruta
[baguhin | baguhin ang wikitext]- Mga problema ng daang Hamiltonian at siklo
- Minimum spanning tree
- Problema ng route inspection (tinatawag din na "Ang Problema ng Karterong Tsino")
- Pitong Tulay ng Königsberg
- Problema ng pinakamaigsing path
- Steiner tree
- Problema ng tatlong-cottage
- Problema ng naglalakbay na manlalako (NP-complete)
Network flow
[baguhin | baguhin ang wikitext]Maraming problema na umuusbong lalo na sa mga applikasyong may kinalaman sa iba-ibang ideya hinggil sa flow ng mga network, halimbawa:
- Max flow min cut theorem
Mga problema ng visibility graph
[baguhin | baguhin ang wikitext]- Problema ng guwardiya ng museyo
Covering na problema
[baguhin | baguhin ang wikitext]Ang mga covering na problema ay ispesipikong pag-iral ng problema ng subgraph-finding, at malapit ito sa mga problemang clique o problemang independent set.
- Problema ng set cover
- Problema ng vertex cover
Aplikasyon
[baguhin | baguhin ang wikitext]Ang aplikasyon ng teoriyang grap ay pangunahin, ngunit hindi esklusibong may kinalaman sa mga labeled graph at iba pang espesiyalisasyon ng mga ito.
Maraming istruktura ang maikakatawan ng grap, at maraming problema na praktikal ang maikakatawan ng grap. Ang istruktura ng mga kawing ng isang websayt ay maaaring ikatawan ng isang directed graph: ang mga taluktok ang mga pahina na nasa websayt at ang isang may-direksiyong dulo mula pahina A papunta sa pahina B na umiiral lamang kung at tangi kung ang A may kawing na papunta sa B. Maaring gumamit ng katulad nitong dulog sa mga problema sa paglalakbay, biyolohiya, pagdidisenyo ng mga tatal pangkompyuter (computer chip), at iba pang larangan. Samakatuwid ang pagpapaunlad ng mga algoritmo sa pagmanipula ng mga grap ay isang mahalagang bagay sa agham ng kompyuter.
Maaaring palawigin ang isang istruktura ng grap sa pamamagitan ng pag-asayn ng timbang sa bawat dulo ng grap. Ang mga grap na may timbang ay ginagamit sa pagkatawan sa mga istruktura na ang mga koneksiyon ng pares ay may kung anong halagang numero. Halimbawa kung ang grap ay kumakatawan sa isang lambat-lambat (network) ng mga kalye, ang timbang ay maaaring kumatawan sa haba ng bawat kalye. Ang isang digraph na may tinimbangang dulo sa konteksto ng teoriyang grap ay tinatawag na lambat-lambat.
Ang mga lambat-lambat ay maraming gamit sa praktikal na panig ng teoriyang graph, ang pag-analisa ng network (halimbawa, sa paggawa ng modelo at pagsusuri ng mga lambat-lambat ng trapiko). Sa pag-aanalisa ng lambat-lambat ang kahulugan ng terminong "network" ay paiba-iba, at maaaring kadalasan ay tumutukoy lamang sa isang simpleng grap.
Maraming aplikasyon ng teoriyang graph ang nasa anyo ng pag-analisa ng lambat-lambat. Nahahati ito sa tatlong kategoriya. Una, ang pag-analisa upang matukoy ang istruktural na katangian ng isang lambat-lambat, tulad ng distribusyon ng mga antas (degree) ng taluktok at ang bantod ng grap. Maraming makikitang sukat ng graph, at ang paglikha ng mga kapakipakinabang na panukat para sa iba't-ibang domain ay nananatiling aktibong larangan ng pananaliksik. Pangalawa, ang pag-analisa upang makatagpo ng masusukat na kantidad sa loob ng network, halimbawa, para sa isang network ng transportasyon, ang antas ng daloy ng sasakyan sa anumang porsiyon nito. Pangatlo, pagsusuri ng dinamikong katangian ng mga network.
Ang teoriyang grap ay ginagamit din sa pag-aaral ng mga molekula sa sa kimika at pisika. Sa condensed matter na pisika, ang may tatlong dimensiyong istruktura ng mga komplikadong simulated atomic structure ay mapag-aaralan nang pakantitatibo sa pamamagitan ng pangangalap ng mga estadistika sa mga katangiang pangteoriyang graph na may kaugnayan sa topolohiya ng mga atom. Halimbawa ang mga shortest-path (SP) rings ni Franzblau. Sa kimika ang grap ay isang natural na modelo para sa isang molekula, kung saan ang mga taluktok ay kumakatawan sa mga atom at ang mga dulo ang bond. Ang dulog na ito ay ginagamit sa pagproseso sa pamamagitan ng kompyuter ng mga istruktura ng molekula, mula editor na pangkimika hanggang sa paghahanap sa database.
Ang teoriyang grap ay malawakan ding ginagamit sa sosyolohiya bilang paraan, halimbawa, sa pagsukat ng reputasyon ng aktor o sa paggalugad ng mga mekanismo ng diffusion, lalo na sa pamamagitan ng mga software na pang-analisa ng social network.
Mga sanggunian
[baguhin | baguhin ang wikitext]- Claude Berge|Berge, Claude, Théorie des graphes et ses applications. Collection Universitaire de Mathématiques, II Dunod, Paris 1958, viii+277 pp. (English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition. Dover, New York 2001)
- Pelle, Stéphane (1996), La Théorie des Graphes (PDF), Saint-Mandé: École Nationale des Sciences Géographiques, inarkibo mula sa orihinal (PDF) noong 2006-12-01, nakuha noong 2008-08-06
{{citation}}: CS1 maint: date auto-translated (link) - Chartrand, Gary, Introductory Graph Theory, Dover. ISBN 0-486-24775-9.
- Biggs, N.; Lloyd, E. & Wilson, R. Graph Theory, 1736-1936 Oxford University Press, 1986
- Harary, Frank, Graph Theory, Addison-Wesley, Reading, MA, 1969.
- Harary, Frank, and Palmer, Edgar M., Graphical Enumeration (1973), Academic Press, New York, NY.
Mga sanggunian
[baguhin | baguhin ang wikitext]- ↑ Biggs, N.; Lloyd, E. and Wilson, R. (1986). Graph Theory, 1736-1936. Oxford University Press.
{{cite book}}: CS1 maint: date auto-translated (link) CS1 maint: multiple names: mga may-akda (link) - ↑ Cauchy, A.L. (1813). "Recherche sur les polyèdres - premier mémoire". Journal de l'Ecole Polytechnique. 9 (Cahier 16): 66–86.
{{cite journal}}: CS1 maint: date auto-translated (link) - ↑ L'Huillier, S.-A.-J. (1861). "Mémoire sur la polyèdrométrie". Annales de Mathématiques. 3: 169–189.
{{cite journal}}: CS1 maint: date auto-translated (link) - ↑ Cayley, A. (1875). "Ueber die Analytischen Figuren, welche in der Mathematik Bäume genannt werden und ihre Anwendung auf die Theorie chemischer Verbindungen". Berichte der deutschen Chemischen Gesellschaft. 8: 1056–1059. doi:10.1002/cber.18750080252.
{{cite journal}}: CS1 maint: date auto-translated (link) - ↑ Sylvester, J.J. (1878). "Chemistry and Algebra". Nature. 17: 284. doi:10.1038/017284a0.
{{cite journal}}: CS1 maint: date auto-translated (link) - ↑ Appel, K. and Haken, W. (1977). "Every planar map is four colorable. Part I. Discharging". Illinois J. Math. 21: 429–490.
{{cite journal}}: CS1 maint: date auto-translated (link) CS1 maint: multiple names: mga may-akda (link) - ↑ Appel, K. and Haken, W. (1977). "Every planar map is four colorable. Part II. Reducibility". Illinois J. Math. 21: 491–567.
{{cite journal}}: CS1 maint: date auto-translated (link) CS1 maint: multiple names: mga may-akda (link) - ↑ Robertson, N.; Sanders, D.; Seymour, P. and Thomas, R. (1997). "The four color theorem". Journal of Combinatorial Theory Series B. 70: 2–44. doi:10.1006/jctb.1997.1750.
{{cite journal}}: CS1 maint: date auto-translated (link) CS1 maint: multiple names: mga may-akda (link)



![{\displaystyle d_{x,y}=\min\{n\mid A^{n}[x,y]\neq 0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9547579b9ea9efe2fadb58a0958466b96c5a47df)

