Salubungan (matematika)


Tulungang mapabuti po ito sa pamamagitan ng pagdagdag ng mga pagsipi sa mga sangguniang mapagkakatiwalaan. Tandaan lamang po na maaari pong mapagdudahan at matanggal ang mga hindi beripikadong nilalaman. |
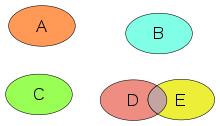
Sa matematika, ang salubungan (Ingles: intersection) o interseksiyon (mula Kastila intersección) ng dalawa o higit pang bagay ay isa pang (madalas na) "mas maliit" na bagay. Sa madaling salita, ang salubungan ng mga bagay ay ang lahat ng mga bagay na parehong meron sila. Halimbawa, sa heometriyang Euclidyano, kapag di magkahilera ang dalawang linya sa isang lapya, ang salubungan nilang dalawa ay ang puntong nagbanggaan sila. Sa pangkalahatang paliwanag, sa teorya ng pangkat, ang salubungan ng dalawang pangkat ay ang pangkat ng mga elementong pareho silang meron. Di tulad ng kahulugan nito sa heometriyang Euclidyano, hindi nito ipinagpapalagay na ang mga bagay na tinutukoy ay nakalagay sa iisang espasyo.
Isa sa mga pangunahing konsepto sa heometriya ang salubungan. Maaaring magkaroon ng samu't saring mga hugis ang isang salubungan, pero mas madalas gamitin ang punto sa larangan ng heometriyang panglapya. Sa heometriyang pang-insidente, ang salubungan ay isang bagay (madalas, mga patag) ng mas mababang dimensiyon na isang insidente sa bawat isang orihinal na bagay. Dahil sa kahulugang ito, maaaring undefined ang mga salubungan, katulad ng kaso ng mga linyang magkahilera (parallel lines). Sa parehong kaso, dumedepende sa lohikal na kasabayan ang konsepto ng salubungan. Samantala, ginagamit naman sa heometriyang alhebraiko ang teorya ng salubungan para bigyang-kahulugan ito.
Kawing panlabas
[baguhin | baguhin ang wikitext]- Weisstein, Eric W. "Salubungan". MathWorld (sa wikang Ingles).
