Estadistika
Ang estadistika (Ingles: statistics) ay ang pag-aaral tungkol sa pagtitipon, pagsasaayos, pag-aanalisa o pagsisiyasat, pagbibigay kahulugan o interpretasyon at pagtatanghal ng mga datos (o data). [1][2] Kabilang dito ang pagpaplano ng pagkuha o koleksiyon ng datos ayon sa disenyo o paraan ng mga estadistikal na survey at disenyong eksperimental.[1] Ang isang estadistiko (statistician) ay maalam sa mga paraan na kailangan para sa matagumpay na aplikasyon ng analisis na estadistikal. Ang gayong mga tao ay kadalasang nagkakamit ng karanasan sa pamamagitan ng paggawa sa anuman sa mga malawak na larangan. Mayroon ding isang disiplinang tinatawag na estadistikang matematikal na nag-aaral ng estadistika ng matematikal. Ang salitang statistics kapag tumutukoy sa disiplinang pang-agham ay pang-isahan o singular gaya ng sa "Statistics is an art."[3] Ito ay hindi katulad ng salitang statistic na tumutukoy sa kantidad gaya ng mean at median na kinukuwenta mula sa mga datos,[4] na ang plural ay statistics.
Buod
[baguhin | baguhin ang wikitext]Sa paggamit ng estadistika sa isang problemang pang-siyentipiko, industriyal, o panlipunan, kailangang magsimula sa isang populasyong estadistikal. Ang populasyon ay maaaring iba ibang paksa gaya ng "lahat ng mga taong nabubuhay sa isang bansa" o "ang bawat atomo na bumubuo sa isang kristal". Ang isang populasyon ay maaaring binubuo ng mga obserbasyon ng isang proseso sa iba't ibang mga panahon na ang datos sa bawat obserbasyon ay nagsisilbi bilang isang ibang pangkat ng pangkalahatang pangkat. Ang datos o data na nakolekta tungkol sa uring ito ng populasyon ay bumubuo ng tinatawag na serye ng panahon. Para sa mga dahilang praktikal, ang isang napiling pang-ilalim na hanay ng populasyon na tinatawag na sampol(sample) ay pinag-aaralan — kabaligtran ng pagtitipon ng datos tungkol sa buong pangkat(isang operasyon na tinawag na censo). Kapag ang sampol na kumakatawan sa populasyon ay natukoy, ang datos ay titipunin para sa mga pangkat ng sampol sa isang obserbasyonal o eksperimental na pagtatakda. Ang datos na ito ay isasailalim naman sa pagsisiyasat na estadistikal na nagsisilbi sa dalawang magkaugnay na mga layunin: deskripsiyon(paglalarawan) at imperensiya(paghihinuha).
- Ang estadistikang deskriptibo o estadistikang naglalarawan ay nagbubuod ng mga datos ng populasyon sa pamamagitan ng paglalarawan kung ano ang napagmasdan sa sampol ng numerikal o grapikal. Ang mga deskriptor na numerikal ay kinabibilangan ng mean at pamangtayang paglihis(standard deviation) para sa tuloy tuloy na distribusyong probabilidad na mga uri tulad ng taas o timbang samantalang ang prekwensiya at persentahe ay mas magagamit ayon sa paglalarawan ng datos na kategorikal tulad ng lahi.
- Ang estadistikang imperensiyal o estadistikang paghihinuha ay gumagamit ng mga pattern sa mga datos na sampol upang humango ng mga konklusyon tungkol sa populasyong kinakatawan na sumasailalim sa random na mga bariasyon o pagkakaiba. Ang mga imperensiyang ito ay maaaring kumuha ng anyong: pagsagot ng mga tanong na oo/hindi tungkol sa datos(pagsubok ng hipotesis), pagtatantiya ng mga katangiang numerikal ng datos(teoriyang estimasyon), paglalarawan ng mga ugnayan sa loob ng korelasyon at pagmomodelo ng mga ugnayan sa loob ng datos(halimbawa gamit ang analis na regresyon). Ang inperensiya ay maaaring palawigin sa forecasting, paghula at estimasyon ng mga hindi naobserbahang halaga sa o nauugnay sa populasyong pinag-aaralan. Ito ay maaaring kabilangan ng ekstrapolasyon at interpolasyon ng seryeng panahon o datos na pang-espasyo at maaari ring kabilangan ng pagmimina ng datos.[5]
Ang konsepto ng korelasyon ay partikular na kapansin pansin para sa potensiyal na kalituhang maaaring sanhiin nito. Ang analisis na estadistikal ng datos ng isang hanay ng datos ay kadalasang naghahayag na ang dalawang mga variable(katangian) ng populasyon sa ilalim ng konsiderasyon ay may kagawiang magbago ng sabay na parang ang mga ito ay magkaugnay. Halimbawa, sa isang pag-aaral ng taunang sahod na tumitingin rin sa edad ng kamatayan, maaaring matagpuan na ang mahihirap na tao ay may kagawiang magkaroon ng mas maikling buhay kesa sa mga mayamang tao. Ang dalawang mga variable ay sinasabing korelado. Gayunpaman, ang mga ito ay maaari o hindi maaaring sanhi ng isa pa. Ang penomenang korelasyon ay maaaring sinanhi ng isang ikatlo na nakaraang hindi isinaalang alang na phenomenon na tinatawag na nagkukubling variable o nakalilitong variable. Dahil dito, walang paraan na agarang mahinuha ang pag-iral ng isang ugnayang nagsasanhi sa pagitan ng dalawang mga variable. Para sa isang sampol na gamitin bilang isang gabay sa isang buong populasyon, mahalagang ito ay tunay na representatibo ng kabuuang populasyon. Ang pagsasampol na representatibo ay sumisiguro na ang mga inperensiya at mga konklusyon ay ligtas na mapapalawig mula sa sampol tungo sa populasyon bilang kabuuan. Ang isang pangunahing problema ay nasa pagtukoy ng sakop kung saan ang napiling sampol ay talagang representatibo. Ang estadistika ay nagaalok ng mga paraan upang tantiyahin at ituwid ang anumang randomang pagggawi sa loob ng sampol at mga pamamaraan ng pagtitipon ng datos. Mayroon ding mga pamamaraan ng disenyong eksperimental para sa mga eksperimento na magpapabawas ng mga isyung ito sa simula ng pag-aaral na nagpapalakas ng kakayahan nito sa pagtukoy ng katotohanan tungkol sa populasyon. Ang pagiging randoma ay pinag-aaralan gamit ang disiplinang matematikal ng teoriya ng probabilidad. Ang probabilidad ay ginagamit sa estadistikang matematikal(alternatibong teoriyang estadistikal upang pag-aralan ang mga distribusyong ng pagsasampol ng estadistikang sampol at sa mas pangkalahatan ang mga katangian ng mga pamamaraang estadistikal. Ang paggamit ng anumang pamamaaraang estadistikal ay balido kapag ang sistema o populasyon na nasa ilalim ng pagsasaalang alang ay sumasapat sa mga asumpsiyon ng paraan. Ang hindi tamang paggamit ng estadistika ay maaaring lumikha ng hindi madaling matukoy ngunit mga seryosong pagkakamali sa deskripsiyon at interpretasyon. Halimbawa, ang patakarang panlipunan, pagsasanay medikal, at pagiging maaasahan ng mga tulay ay lahat umaasa sa angkop na paggamit ng estadistika. Kahit pa ang mga pamamaraang estadistikal ay tamang inilapat, ang mga resulta ay maaaring mahirap na bigyan ng pakahulugan para sa mga walang kadalubhasaan. Ang kahalagahang estadistikal ng isang kagawian sa datos na sumusukat sa sakop kung saan ang isang kagawian ay maaaring sanhi ng isang randomang bariasyon sa sampol ay maaari o hindi maaaring umayon sa intuitibong kahulugan ng kahalagahan nito. Ang hanay ng mga basikong kasanayang estadistikal at skeptisisismo na kailangang pakitunguhan ng mga tao sa impormasyon sa bawat araw ng kanilang buhay ng angkop ay tinutukoy na literasiyang estadistikal.
Mga pamamaraang estadistikal
[baguhin | baguhin ang wikitext]Mga pag-aaral eksperimental at obserbasyonal
[baguhin | baguhin ang wikitext]Ang isang karaniwang layunin pasa dalawang mga uri ay nasa kung paanong ang pag-aaral ay aktuwal na isinagawa. Ang bawat isa ay maaaring napaka epektibo. Ang isang pag-aaral eksperimental ay maaaring kasangkutan ng pagkuha ng mga sukat ng sistemang pinag-aaralan na nagmamanipula sa sistema at pagkatapos ay kumukuha ng karagdagang mga pagsukat gamit ang parehong pamamaraan upang tukuyin kung ang manipulasyon ay nagpabago sa mga halaga ng mga sukat. Bilang salungat dito, ang isang pag-aaral obserbasyonal ay hindi sumasangkot sa eksperimental na manipulasyon. Bagkus, ang datos ay tinitipon at ang mga korelasyon sa pagitan ng mga prediktor at tugon ay iniimbestigahan.
Mga eskperimento
[baguhin | baguhin ang wikitext]Ang mga basikong hakbang ng isang eksperimentong estadistikal ang sumusunod:
- Pagpaplano ng pagsasaliksik kabilang ang paghahanap ng bilang ng mga replikado ng pag-aaral gamit ang sumusunod na impormasyon: preliminaryong mga pagtatantiya tungkol sa sukat ng mga epekto ng pagtatrato, alternatibong hipotesis at ang tinantiyang eksperimental na variability. Ang pagsasaalang alang ng pagpili ng mga paksang eksperimental at ang mga etika ng pagsasaliksik ay kinakailangan. Ang mga estadistiko ay nagrerekomiyenda na ang mga eksperimento ay kumukumpara(kahit papaano) sa isang bagong pagtatrato sa isang pamantayang pagtatrato o kontrol upang payagan ang walang kinikilingang pagtatantiya ng pagkakaiba sa mga epekto ng pagtatrato.
- Disenyo ng mga eksperimento gamit ang pagbobloke upang bawasan ang impluwensiya ng nakalilitong variable at randomisadong pagtatakda ng mga pagtatrato ng paksa upang payagan walang kinikilingang mga pagtatantiya ng mga pagtatratong epekto at pagkakamaling eksperimental. Sa yugtong ito, ang mga nageeksperimento at statitistiko ay sumusulat ng eksperimental na protokol na gagabay sa pagsasagawa ng eksperimto at tutukoy ng pangunahing analis ng datos eksperimental.
- Pagsasagawa ng eksperimento kasunod ng eksperimental na protokol at pagsusuri ng datos kasunod ng eksperimental na protokol.
- Karagdagang pagsisiyasata ng hanay ng datos sa isang ikalawang analisis upang magmungkahi ng bagong hipotesis para sa panghinaharap na pag-aaral.
- Pagdodokumento at pagpepresenta ng mga resulta ng pag-aaral.
Ang mga eksperimento sa pag-aasal ng tao ay may espesyal na mga pagkabahala. Ang sikat na pag-aaral Hawthorne ay sumuri ng mga pagbabago sa gumagawang kapaligiran sa plantang Hawthorne ng Western Electric Company. Ang mga mananaliksik ay interesado sa pagtukoy kung ang tumaaas na iluminasyon(liwanag) ay magdadagdag ng produktibididad ng mga trabahador ng linyang pagaasembleo. Unang sinukat ng mga mananaliksik ang produktibidad sa planta at pagkatapos ay binago ang liwanag sa area ng planta at tiningnan kung ang mga pagbabago sa liwanag ay umapekto sa produktibidad. Lumabas na ang produktibidad ay talagang nagpabago(sa ilalim ng mga kondisyong eksperimental). Gayunpaman, ang pag-aaral ay labis na binatikos ngayon dahil sa mga pagkakamali sa mga pamamaraang eksperimental, spesipiko na ang kawalan ng pangkat na kontrol at pagiging bulag. Ang epektong Hawthorne ay tumutukoy sa pagkakatuklas na ang kinalabasan(sa kasong ito ang produktibidad ng trabahador) ay nagbago sanhi ng mismong obserbasyon. Ang mga nasa pag-aaral Hawthorne ay naging mas produktibo hind dahil sa ang liwanag ay binago kundi ang mga ito ay pinagmasdan.
Pag-aaral obserbasyonal
[baguhin | baguhin ang wikitext]Ang isang halimbawa ng pag-aaral oberbasyonal ang isa na gumagalugad sa korelasyon sa pagitan ng pagsisigarilyo at kanser sa baga. Ang uri ng pag-aaral na ito ay karaniwang gumagamit ng mga survery upang magtipon ng mga oberbasyon tungkol sa sakop ng interes at pagkatapos ay magsasagawa ng mga analisis na estadistikal. Sa kasong ito, ang mga mananaliksik ay magtitipon ng mga oberbasyon ng parehong mga nagsisigarilyo at hindi nagsisigarilyo, marahil sa pamamagitan ng isang pag-aaral ng kasong kontrol at pagkatapos ay titingin para sa bilang ng mga kaso ng kanser sa bago sa bawat pangkat.
Mga lebel ng sukat
[baguhin | baguhin ang wikitext]Mayroong apat na pangunahing mga level ng sukat na ginagamit sa estadistika: nominal, ordinal, interbal at rasyo[6]. Ang bawat isa sa mga ito ay may iba't ibang mga digri ng paggamit sa pagsasaliksik estadistikal. Ang mga pagsukat na rasyo ay parehong mayroong makahulugang halagang sero at ang distansiya sa pagitan ng mga pagkakaibang sukat ay inilarawan. Ang mga ito ay nagbibigay ng pinakadakilang pleksibilidad sa mga pamamaraang estadistikal na maaaring gamit sa pagsusuri ng datos. Ang mga pagsukat interbal ay may mga makahulugang mga distansiya sa pagitan ng mga sukat na inilarawan ngunit ang halagang sero ay arbitraryo(gaya ng sa kaso ng longhitud at mga sukat ng temperatura sa Celsius o Fahrenheit). Ang mga pagsukat ordinal ay may hindi tiyak na pagkakaiba sa pagitan ng mga sunod sunod na halaga ngunit may makahulugang kaayusan sa mga halagang ito. Ang mga sukat nominal ay walang makahulugang ranggong kaayusan sa mga halaga. Dahil sa ang mga variable na umaayon lamang nominal o ordinal na pagsukat ay hindi makatwirang masusukat ng numerikal, minsan ang mga ito ay pinapangkat ng sabay sabay bilang mga kategorikal na variable samantalang ang mga sukat rasyo at interbal ay pinapangkat ng sabay sabay bilang mga kwantitatibong variable na maaaring diskreto o tuloy tuloy sanhi ng kalikasan numerikal ng mga ito.
Mga mahalagang terminong ginagamit sa estadistika
[baguhin | baguhin ang wikitext]Hipotesis na null
[baguhin | baguhin ang wikitext]Ang interpretasyon ng impormasyong estadistikal ay kadalasang sumasangkot sa pagpapaunlad ng isang hipotesis na null(null hypothesis) dahil sa ang asumpsiyon ay kung ano ang minumungkahing sanhi ay walang epekto sa variable na sinusukat. Ang mahusay na ilustrasyon para sa isang baguhan ang predikamentong naeenkwentro sa isang paglilitis ng hurado. Ang hipotesis na null na H0 ay nagsasaad na ang isinasakdal ay inosente samantalang ang altenatibong hipotesis na H1 ay nagsasaad na ang sinasakdal ay may sala. Ang pagkakaso ay dumarating dahil sa pagsusupetsa ng pagkakaroon ng sala. Ang H0 (status quo) ay nakatayong sumasalungat sa H1 at pinapanatili malibang ang H1 ay sinusuportahan ng ebidensiya ng "lagpas sa makatwirang pagdududa". Gayunpaman, ang "pagkabigo na itakwil ang H0" sa kasong ito ay hindi nagpapahiwatig ng pagiging inosente ngunit tanging ang ebidensiya ay hindi sapat upang hatulan ang isinasakdal. Kaya ang hurado ay hindi kinakailangang tumangap ng H0 ngunit nabibigong tumawkil sa H0. Bagaman hindi mapapatunayan ang isang hipotesis na null, ang isa ay maaaring sumubok kung paanong kalapit ito sa pagiging totoo sa isang kapangyarihang estadistikal na sumusubok para sa uring II mga pagkakamali.
Pagkakamali
[baguhin | baguhin ang wikitext]Sa paggawa mula sa isang hipotesis na null, ang dalawang mga basikong anyo ng pagkakamali ay kinikilala:
- Uring I mga pagkakamali kung saan ang hipotesis na null ay maling itinakwil na nagbibigay ng isang "maling positibo".
- Uring II mga pagkakamali kung saan ang hipotesis na null ay nabibigong maitakwil at ang isang aktuwal na pagkakaiba sa pagitan ng mga populasyon ay nakaligtaan na nagbibigay ng isang "maling negatibo".
Ang pagkakamali ay tumutukoy rin sa sakop kung saan ang mga indibidwal na oberbasyon sa isang sampol ay iba mula sa isang sentral na halaga gaya ng sa sampol o mean ng populasyon. Maraming mga pamamaraang estadistikal ay naghahangad na paliitin ang pagkakamaling kinwadradong mean at ang mga ito ay tinatawag na "maliit na mga kwadrado". Ang mga prosesong pagsukat na lumilikha ng datos estadistikal ay sumasailalim rin sa pagkakamali. Marami sa mga pagkakamaling ito ay inuuri bilang randomang pagkakamali(ingay) o sistematikong pagkakamali(pagkiling) ngunit maraming pang mga ibang uri ng mga pagkakamali ay maaari ring mahalaga.
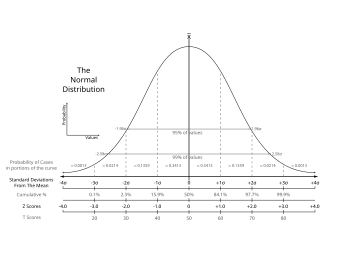
Estimasyon ng interbal
[baguhin | baguhin ang wikitext]Ang karamihan ng mga pag-aaral ay nagsasampol lamang ng isang bahagi ng isang populasyon at kaya ang resulta ay hindi buong representatibo ng buong populasyon. Ang anumang mga pagtatantiyang nakamit mula sa sampol ay tanging nagtatantiya ng halaga ng populasyon. Ang mga interbal ng kompiyansa(confidence interval) ay pumapayag sa mga estadistiko na maghayag kung gaanong kalapit ang pagtatantiya ng sampol ay tumutugma sa tunay na halaga ng buong populasyon. Kadalasan, ang mga ito ay naghahayag bilang 95% na mga interbal ng kompiyansa. Sa pormal na paglalarawan, ang isang 95% interbal ng kompiyansa para sa isang halaga ay isang saklaw kung saan, kung ang pagsasampol at analisis ay inulit sa ilalim ng parehong mga kondisyon(na nagbibigay ng isang ibang hanay ng datos), ang interbal ay kabibilangan ng tunay(populasyon) na halagang 95% ng panahon. Ito ay hindi nagpapahiwatig na ang probabibilidad na ang tunay na halaga ay nasa interbal ng kompiyansa ay 95%. Mula sa perspektibong prekwentista, ang gayong pag-aangkin ay walang saysay dahil ang tunay na halaga ay hindi isang random variable. Ang tunay na halaga ay nasa loob o wala sa loob ng isang ibinigay na interbal. Gayunpaman, totoo na bago ang anumang datos ay sinampol at sa ibinigay na isang plano para sa kung paanong ang kompiyansang interbal ay itatayo, ang probabilidad ay 95% na ang hindi pa nakukwentang interbal ay sasakop sa tunay na halaga. Sa puntong ito, ang mga hangganan sa interbal ay ang mga hindi pa napagmamasdang mga random variable. Ang isang pakikitungo na nagbibigay ng interbal na mapapakahulugang mayroong isang ibinigay na probabilidad ng paglalaman ng tunay na halaga ay ang paggamit ng isang kapaniwa-paniwalang interbal mula sa estadistikang Bayesian. Ang pakikitungong ito ay nakasalalay sa isang ibang paraan ng pagpapakahulugan kung ano ang ibig sabihin ng probabilidad ie bilang isang probabilidad na Bayesian.
Kahalagahan
[baguhin | baguhin ang wikitext]Ang estadistika ay bihirang magbigay ng isang simpleng uring oo/hindi sagot sa tanong na tinatanong dito. Ang interpretasyon ay kadalasang dumarating sa lebel ng kahalagahang estadistikal(statistical significance) na nilalapat sa mga bilang at kadalasang tumutukoy sa probabilidad ng isang halagang tiyak na tumatakwil sa hipotesis na null(minsang tinatawag na halagang-p). Ang pagtukoy sa kahalagahang estadistikal ay hindi kinakailangang mangahulugang ang kabuuang resulta ay mahalaga sa mga termino ng tunay na daigdig. Halimbawa, sa isang malaking pag-aaral ng droga, maaaring ipakita na ang droga ay may mahalagang estadistikal ngunit napaka liit na epektong benepisyal sa paraang ang droga ay hindi malamang na makatulong sa isang pasyente sa isang mapapansing paraan. Ang mga kritisismo ay lumilitaw dahil ang pakikitungong pagsubok ng hipotesis ay pumupwersa sa isang hipotesis(ang hipotesis na null) na paboran at tila rin magpasidhi ng kahalagahan ng maliit na mga pagkakaiba sa malaking mga pag-aaral. Ang isang pagkakaiba na mataas na mahalagang estadistikal ay wala pa ring praktikal na kahalagahan ngunit posibleng angkop na magpormula ng mga pagsubok para dito. Ang isang tugon ay sumasangkot sa paglagpas sa paguulat lamang sa lebel ng kahalagahan upang isama ang halagang-p kapag nag-uulat kung ang isang hipoteiss ay itinakwil o tinanggap. Gayunpaman, ang halagang-p ay hindi nagpapakita ng sukat ng epekto. Ang isang mas mabuti at tumataas na karaniwang pakikitungo ay iulat ang mga interbal ng kompiyansa. Bagaman ang mga ito ay nililikha mula sa parehong mga kalkulasyon gaya ng sa mga pagsubok ng hipotesis o mga halagang p, ang mga ito ay naglalarawan ng parehong sukat ng epekto at kawalang katiyakan na pumapalibot dito.
Mga halimbawa
[baguhin | baguhin ang wikitext]Ang ilang mga mahusay na kilalang mga mga pagsubok at pamamaraan ang sumusunod:
- Analysis of variance(ANOVA)
- Pagsubok na kinwadradong-Chi
- Korelasyon
- Analisis ng paktor
- Mann–Whitney U
- Mean na kwadradong tinimbang na paglihis(MSWD)
- Koepisyenteng Pearson produkto-sandaling korelasyon
- Regresyong analisis
- Koepisyenteng ranggong korelasyon ni Spearman
- Pagsubok na t ni Student
- analisis ng panahong serye
Pagkukwentang estadistikal
[baguhin | baguhin ang wikitext]
Ang mabilis at natustusang pagtaas sa kapangyarihang pagkukuwenta simula ikalawang kalahati ng ika-20 siglo ay nagkaroon ng mahalagang epekto sa pagsasanay ng agham estadistikal. Ang mga sinaunang modelong estadistikal ay halos kadalasang mula sa klase ng mga modelong linyar ngunit ang mga makapangyarihang kompyuter na sinamahan ng mga angkop na algoritmong numerikal ay nagsanhi ng isang tumaas na interes sa mga modelong hindi linyar gaya ng mga network na neural gayundin ang paglikha ng mga bagong uri gaya ng mga nilahat na modelong linyar at mga modelong multilebel. Ang tumaas na kapangyarihang pagkukwenta ay tumungo rin sa lumalagong kasikatan ng komputasyonal na intensibong mga pamamaraan batay sa muling pagsasampol gaya ng mga pagsubok na permutasyon at ang pagbobootsrap samantalang ang mga pamamaraan gaya ng pagsasampol na Gibbs ay gumawa sa mga modelong Bayesian na mas magagawa. Ang rebolusyong kompyuter ay may mga implikasyon para sa hinaharap ng estadistika na may bagong pagbibigay diin sa estadistikang eksperimental at empirikal. Ang isang malaking bilang ng parehong pangkalahatan at espesyal na tungkuling mga sopwer estadistikal ay magagamit na sa kasalukuyan.
Kasaysayan ng agham pang-estadistika
[baguhin | baguhin ang wikitext]
Ang mga kaparaanan pang-estadistika ay tinatayang nagsimula noong ika-5 siglo BC.
May mga dalubhasa ang nagtuturo sa pinagmulan ng estadistika sa 1663, sa lathala ng Natural and Political Observations upon the Bills of Mortality ni John Graunt.[7] Ang mga naunang paglalapat ng kaisipang pang-estadistika ay umiinog sa mga pangangailangan ng estado sa pagbatay sa mga patakaran sa demograpiko at datos pang-ekonomiko, kaya nagmula ang etimolohiya nitong stat-. Ang nasasakop ng disiplina ng estadistika ay napalawak noong unang bahagi ng ika-19 na siglo na sinama ang koleksyon at pagsuri ng datos sa pangkalahatan. Naglaon, nagagamit ang estadistika sa pamahalaan, negosyo at sa mga agham na likas at panlipunan.
Mga sanggunian
[baguhin | baguhin ang wikitext]- ↑ 1.0 1.1 Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9
- ↑ The Free Online Dictionary
- ↑ "Statistics". Merriam-Webster Online Dictionary.
- ↑ "Statistic". Merriam-Webster Online Dictionary.
- ↑ Leo Breiman (2001). "Statistical Modelling: the two cultures", Statistical Science 16 (3), pp.199-231. doi:10.1214/ss/1009213726 MR1874152
- ↑ Thompson, B. (2006). Foundations of behavioral statistics. New York, NY: Guilford Press.
- ↑ Willcox, Walter (1938) "The Founder of Statistics". Review of the International Statistical Institute 5(4):321–328. Padron:Jstor
