Sirkumperensiya
| Heometriya | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||
|
||||||||||
|
Apat- / ibang-dimensiyonal |
||||||||||
| Mga heometra | ||||||||||
|
ayon sa pangalan
|
||||||||||
|
ayon sa panahon
|
||||||||||

Sa heometriya, ang sirkumperensiya (mula sa Latin na circumferens, nangangahulugang "dinadala sa palibot") ay ang perimetro o palibot ng isang bilog o elipse.[1] Alalaong baga, ang sirkumperensiya ay magiging haba ng arko ng bilog, na kapag binuksan at diniretso, magiging segmentong linya.[2] Sa mas pangkalahatan, ang perimetro ay ang habang pakurba sa palibot ng kahit anumang pigurang nakasara. Maaring tukuyin din ng sirkumperensiya ang bilog mismo, alalaong baga, ang locus o lugar na kaayon sa gilid ng isang disko. Ang sirkumperensiya ng isang espera ay ang sirkumperensiya, o haba, ng anumang isa mga makabuluhang bilog nito.
Ang ibang katawagan nito sa Tagalog ay yantas at tikop.[3]
Bilog
[baguhin | baguhin ang wikitext]Ang sirkumperensiya ng isang bilog ay ang layo sa palibot nito, subalit kung, tulad sa maraming pagtratong elementarya, ang layo ay binibigay kahulugan sa mga tuntunin ng mga linyang diretso, hindi maaring gamitin ang depinisyon na ito. Sa ilalim ng ganitong katayuan, maaring ipakahulugan ang sirkumperensiya ng isang bilog bilang ang hangganan ng mga perimetro ng nakasulat na mga regular na poligono bilang ang bilang ng mga gilid na tumataas na walang hanggan.[4] Ginagamit ang katawagang sirkumperensiya kapag sinusukat ang mga bagay na pisikal, gayon din kapag kinukunsidera ang mga anyong heometrikong basal.
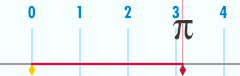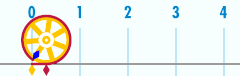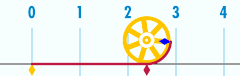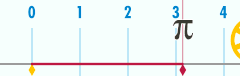

Kaugnayan sa π
[baguhin | baguhin ang wikitext]May kaugnayan ang sirkumperensiya ng isang bilog sa isa sa mga pinakamahalagang konstanteng pangmatematika. Ang konstanteng ito, ang pi (bigkas: pay), ay kinakatawan ng titik Griyego na Ang unang ilang digitong desimal ng halagang numeriko ng ay 3.141592653589793 ...[5] Ikinakahulugan ang pi bilang ang rasyo ng sirkumperensiya ng bilog sa diyametro nito:
O, sa katumbas, bilang ang rasyo ng sirkumperensiya sa doble ng radyo. Maaring muling ayusin ang pormula sa itaas upang lutasin ang sirkumperensiya:
Ang rasyo ng isang sirkumperensiya ng bilog sa radyo nito ay tinatawag ng konstanteng bilog, at katumbas ito ng . Ang halagang ay ang halaga din ng mga radiyan sa isang pihit. Nasa lahat ng dako ng matematika, inhenyeriya, at agham ang konstanteng pangmatematika na π.
Sa Sukat ng isang Bilog na sinulat noong circa 250 BCE ni Arkimedes, pinapakita na ang rasyong ito ( yayamang hindi niya ginamit ang pangalang π) ay higit sa 310/71 subalit mas mababa sa 31/7 sa pamamagitan ng pagkalkula ng mga perimetro ng isang nakasulat at isang tinakdang regular na poligono na may 96 na gilid.[6] Ginamit sa mga dantaon ang kaparaanang ito para sa pagtataya ng π, na kinukuha ang katumpakan sa pamamagitan ng paggamit ng mga poligono ng mas malaki at mas malaking bilang ng mga gilid. Ang pinakahuling ganitong kalkulasyon ay isinagawa noong 1630 ni Christoph Grienberger na gumamit ng mga poligono na may 1040 gilid.
Mga sanggunian
[baguhin | baguhin ang wikitext]- ↑ San Diego State University (2004). "Perimeter, Area and Circumference" (PDF) (sa wikang Ingles). Addison-Wesley. Inarkibo mula sa orihinal (PDF) noong 6 Oktubre 2014.
{{cite web}}: CS1 maint: date auto-translated (link) - ↑ Bennett, Jeffrey; Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (sa wikang Ingles) (ika-3rd (na) edisyon), Addison-Wesley, p. 580, ISBN 978-0-321-22773-7
{{citation}}: CS1 maint: date auto-translated (link) - ↑ Gaboy, Luciano L. Circumference - Gabby's Dictionary: Praktikal na Talahuluganang Ingles-Filipino ni Gabby/Gabby's Practical English-Filipino Dictionary, GabbyDictionary.com.
- ↑ Jacobs, Harold R. (1974), Geometry (sa wikang Ingles), W. H. Freeman and Co., p. 565, ISBN 0-7167-0456-0
{{citation}}: CS1 maint: date auto-translated (link) - ↑ Sloane, N. J. A. (pat.). "Sequence A000796". The On-Line Encyclopedia of Integer Sequences (sa wikang Ingles). OEIS Foundation.
- ↑ Katz, Victor J. (1998), A History of Mathematics / An Introduction (sa wikang Ingles) (ika-2nd (na) edisyon), Addison-Wesley Longman, p. 109, ISBN 978-0-321-01618-8
{{citation}}: CS1 maint: date auto-translated (link)









